A. Student

Math 124 Problem Set 4

1. $\left(\frac{3}{97}\right)={(-1)}^{48}\cdot \left(\frac{97}{3}\right)=\left(\frac{1}{3}\right)=\$1;
$\left(\frac{5}{389}\right)={(-1)}^{2}\cdot \left(\frac{389}{5}\right)=\left(\frac{4}{5}\right)=\$1;
$\left(\frac{2003}{11}\right)=\left(\frac{1}{11}\right)=\$1;
$\left(\frac{5!}{7}\right)=\left(\frac{120}{7}\right)=\left(\frac{1}{7} \right)=\$1;

2. By quadratic reciprocity $\left(\frac{3}{p}\right)={(-1)}^{\frac{p-1}{2}}\cdot \left(\frac{p}{3}\right)$. There are four cases:
Case 1: $p\equiv 1(mod\ 3)$, $p\equiv 1(mod\ 4)$: Then $p\equiv$ 1$(mod\ 12)$ and ${(-1)}^{\frac{p-1}{2}}\cdot \left(\frac{1}{3}\right)=1\cdot 1=\$1.
Case 2: $p\equiv 1(mod\ 3)$, $p\equiv -1(mod\ 4)$: Then $p\equiv$ 7$(mod\ 12)$ and ${(-1)}^{\frac{p-1}{2}}\cdot \left(\frac{1}{3}\right)=-1\cdot 1=\$-1.
Case 3: $p\equiv 2(mod\ 3)$, $p\equiv 1(mod\ 4)$: Then $p\equiv$ 5$(mod\ 12)$ and ${(-1)}^{\frac{p-1}{2}}\cdot \left(\frac{-1}{3}\right)=1\cdot -1=\$-1.
Case 4: $p\equiv 2(mod\ 3)$, $p\equiv -1(mod\ 4)$: Then $p\equiv$ 11$(mod\ 12)$ and ${(-1)}^{\frac{p-1}{2}}\cdot \left(\frac{-1}{3}\right)=-1\cdot -1=\$1.
(We solve the systems with the Chinese Remainder Theorem).

3. It is sufficient to give two distinct elements $a,b$ in $Z_n^*$ of order 2, for if there was a primitive root $g$, then $g^{\phi(2^m)/2}=g^{2^{m-2}}$ cannot simultaneously be congruent to $a$ and $b$ modulo $n$.
Put $a=-1$; since $n>2$, $-1$ has order 2 in $Z_n^*$. Set $b=2^{m-1}-1$; then

$$b^2=(2^{m-1}-1)^2\equiv 2^{2m-2}-2\cdot 2^{m-1}+1\equiv 1(mod\ 2^m).$$

Now $b$ is distinct from $a$, since their difference, $2^{m-1}$, is less than $2^m$. Furthermore, $b\neq 1$, since $m>2$. Therefore $a$ and $b$ are distinct elements of order 2 in $Z_n^*$.

4. Let $g_0$ be a primitive root modulo $p$. We will construct an element $g$ of $Z_{p^2}^*$ with order $\phi(p^2)=p(p-1)$. Let $g=g_0+pt$ for some $t$ to be determined. Then by the binomial theorem

$$g^{p-1}\equiv g_0^{p-1}+(p-1)pg_0^{p-2}t\equiv (1+kp)+p(p-1)g_0^{p-2}t\ (mod\ p^2),$$

for some $k$, since $g_0^{p-1}\equiv 1(mod\ p)$. Now choose $t$ such that $n=k+(p-1)g_0^{p-2}t$ is nonzero modulo $p$. We can do this because $p-1$ and $g_0^{p-2}$ are both elements of $Z_{p}^*$. Then $g^{p-1}\equiv 1+np\ (mod\ p^2)$, $p\nmid n$. Therefore the order of $g$ in $Z_{p^2}^*$ does not divide $p-1$. But it divides $p(p-1)$, and $p$ is prime, so the order of $g$ must be $p(p-1)$. Thus $g$ is a primitive root modulo $p^2$.

5. Let $g$ be a primitive root modulo $p$. Since $p\equiv 1(mod\ 3)$, $c=g^{(p-1)/3}$ has order 3. Therefore $c$ is a solution to $x^3-1=(x-1)(x^2+x+1)=0$ modulo p. Since $c\neq 1$ and we are in a domain, $c^2+c+1=0$. Now note that $4c^2+4c+4=(2c+1)^2+3=0$; therefore $(2c+1)^2=-3$, so $\left(\frac{-3}{p}\right)=1$.

6. The proof is almost identical to the one above. Let $c$ in $Z_p^*$ be an element of order 5. Then $c^5-1=(c-1)(c^4+c^3+c^2+c+1)=0$ and $c\neq 1$ implies that $c^4+c^3+c^2+c+1=0$. Now

$$(c+c^4)^2+(c+c^4)-1=c^2+c^8+2c^5+c+c^4-1=c^4+c^3+c^2+c+1=0.$$

Therefore $(2(c+c^4)+1)^2=4((c+c^4)^2+(c+c^4)-1)+5=5$, so $\left(\frac{5}{p}\right)=1$.

7. All odd primes. Let $p$ be an odd prime and $g$ a primitive root modulo $p$. Rewrite the sum as:

$$\sum_{a=1}^{p-1}{\left(\frac{a}{p}\right)}=\sum_{i=1}^{p-1}{\left... ...\frac{g^{2j}}{p}\right)}= \frac{p-1}{2}\left(1+\left(\frac{g}{p}\right)\right).$$

Now $\left(\frac{g}{p}\right)=-1$, for if $\left(\frac{g}{p}\right)=1$ then $g^{\frac{p-1}{2}}=1$, and $g$ would not be primitive. Therefore $\sum_{a=1}^{p-1}{\left(\frac{a}{p}\right)}=0$.

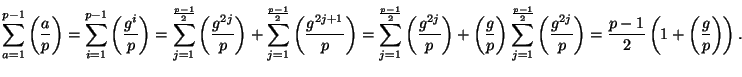
8. A good guess seems to be $C\thickapprox .374$. In PARI, we can write a program to check the first $n$ primes to see if 2 is a primitive root, and divide this total by $n$ to see the behavior of the ratio:
g0(n)=numRoot=0; lPr=prime(2);

for(j=2,n,(if(znorder(Mod(2,lPr))==lPr-1,numRoot++)); lPr=prime(j+1)); tPr=n;

return(numRoot/(1.0*n));
Using this, we have $g0(41560)\thickapprox.37377$. This exhausts PARI's list of primes, so we can write another program to continue testing:

g(n)=lPr=nextprime(lPr+1);

for(j=1,n,(if(znorder(Mod(2,lPr))==lPr-1,numRoot++));tPr++;lPr=nextprime(lPr+1));

return(numRoot/(1.0*tPr));
With this program, we can check the first $n$ primes (according to PARI's nextprime function). For the first 81,560 primes, we have $C\thickapprox.373725$; For the first 101,560 primes, we have $C\thickapprox.374714$. Finally, for the first 200,000 primes, we have $C\thickapprox.374075$.