


Next: About this document ...
A. Student
Math 124 Problem Set 5
2. We establish both identities by induction.
Claim:
![$ [a_n,a_{n-1},\ldots,a_1,a_0]=\frac{p_n}{p_{n-1}}$](img1.png) .
.
Since 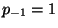 and
and 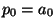 ,
,
![$ [a_0]=\frac{p_0}{p_{-1}}$](img4.png) . This establishes the base case. Now
suppose that
. This establishes the base case. Now
suppose that
![$ [a_{n-1},\ldots,a_0]=\frac{p_{n-1}}{p_{n-2}}$](img5.png) . Then
. Then
![$ [a_n,a_{n-1},\ldots,a_0]=a_n+1/[a_{n-1},\ldots,a_0]=a_n+\frac{1}{\frac{p_{n-1}}{p_{n-2}}}
= a_n+\frac{p_{n-2}}{p_{n-1}}=\frac{a_np_{n-1}+p_{n-2}}{p_{n-1}}$](img6.png) .
The numerator is just the definition of
.
The numerator is just the definition of 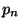 ; this proves the
claim.
; this proves the
claim.
Claim:
![$ [a_n,a_{n-1},\ldots,a_1]=\frac{q_n}{q_{n-1}}$](img8.png) .
.
Since 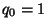 and
and 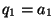 ,
,
![$ [a_1]=\frac{q_1}{q_0}$](img11.png) . This establishes the base case. Now
suppose that
. This establishes the base case. Now
suppose that
![$ [a_{n-1},\ldots,a_1]=\frac{q_{n-1}}{q_{n-2}}$](img12.png) . Then
. Then
![$ [a_n,a_{n-1},\ldots,a_1]=a_n+1/[a_{n-1},\ldots,a_1]=a_n+\frac{1}{\frac{q_{n-1}}{q_{n-2}}}
= a_n+\frac{q_{n-2}}{q_{n-1}}=\frac{a_nq_{n-1}+q_{n-2}}{q_{n-1}}$](img13.png) .
The numerator is just the definition of
.
The numerator is just the definition of 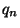 ; this proves the
claim.
; this proves the
claim.
3. If we compute 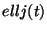 in PARI, where
in PARI, where
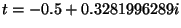 the result is
the result is
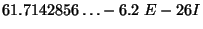 . The imaginary part is effectively 0, so we wish to guess
the rational number that gives the real part. The command
. The imaginary part is effectively 0, so we wish to guess
the rational number that gives the real part. The command
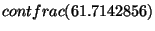 gives
gives
![$ [61,1,2,2,178571]$](img19.png) , suggesting that
a good guess for our rational number is given by the continued
fraction
, suggesting that
a good guess for our rational number is given by the continued
fraction
![$ [61,1,2,2]$](img20.png) . This value is
. This value is
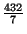 .
.
4i. Let
![$ \alpha=[\overline{2,3}]$](img22.png) . Then
. Then
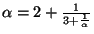 , so
, so
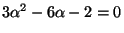 . Solving for
. Solving for 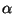 yields
yields
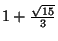 .
.
4ii. First we compute
![$ \alpha=[\overline{1,2,1}]$](img27.png) . This
gives
. This
gives
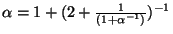 . Solving for
. Solving for
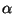 yields
yields
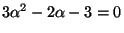 , so
, so
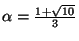 . Now
. Now
![$ [2,\overline{1,2,1}]=2+\frac{1}{[\overline{1,2,1}]}$](img31.png) , so our
final answer is
, so our
final answer is
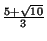 .
.
4iii. This is
![$ [\overline{1,2,3}]^{-1}$](img33.png) . As above, if
. As above, if
![$ \alpha=[\overline{1,2,3}]$](img34.png) then
then
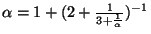 . This
simplifies to
. This
simplifies to
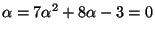 , so
, so
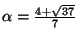 . Therefore our desired answer is
. Therefore our desired answer is
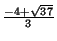 .
.
5. For all three parts we use contfrac in PARI to find
the continued fraction and prove that the answer is correct.
5i. We claim that
![$ \sqrt{5}=[2,\overline{4}]$](img39.png) . Let
. Let
![$ \alpha=[\overline{4}]$](img40.png) ; then
; then
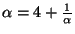 , so
, so
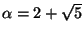 . Now
. Now
![$ [2,\overline{4}]=2+\frac{1}{2+\sqrt{5}}=\sqrt{5},$](img43.png) as desired.
as desired.
5ii. We claim that
![$ \frac{1+\sqrt{13}}{2}=[2,\overline{3}]$](img44.png) . Let
. Let
![$ \alpha=[\overline{3}]$](img45.png) ; then
; then
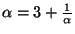 , so
, so
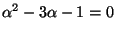 . This gives
. This gives
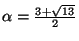 . Then
. Then
![$ [2,\overline{3}]=2+\frac{2}{3+\sqrt{13}}=\frac{1+\sqrt{13}}{2}.$](img49.png)
5iii. We claim that
![$ \frac{5+\sqrt{37}}{4}=[\overline{2,1,3}]$](img50.png) . Let
. Let
![$ \alpha=[\overline{2,1,3}]$](img51.png) ; then
; then
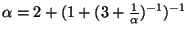 , so
, so
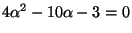 . Solving for
. Solving for 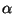 gives
gives
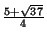 , as desired.
, as desired.
6i. First we compute
![$ [\overline{2n}]$](img55.png) . Let
. Let
![$ \alpha=\overline{[2n]}$](img56.png) ; then
; then
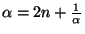 . This
gives
. This
gives
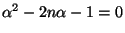 , so
, so
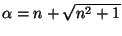 . Now
. Now
![$ [n,\overline{2n}]=n+\frac{1}{\alpha}=n-(n-\sqrt{n^2+1})=\sqrt{n^2+1},$](img60.png) as desired.
as desired.
6ii. Using the previous part, we know that
![$ \sqrt{5}=[2,\overline{4}]$](img39.png) . We can try successive convergents
until two agree up to four decimal places; once such convergent
is
. We can try successive convergents
until two agree up to four decimal places; once such convergent
is 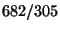 .
.
7. In PARI, use convergents(contfrac(Pi)) to obtain the
convergents of the continued fraction of 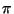 . We can now test
convergents for property described in the problem, noting that
smaller denominators are more likely to work. One convergent
that satisfies the property is
. We can now test
convergents for property described in the problem, noting that
smaller denominators are more likely to work. One convergent
that satisfies the property is 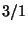 , since
, since 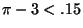 and
and
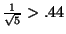 . The next is
. The next is 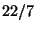 , since
, since
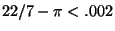 and
and
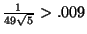 . A third is
. A third is
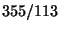 , since
, since
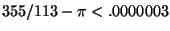 while
while
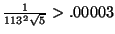 .
.
8. In PARI, the command contfrac(exp(2)) gives
![$\displaystyle [7,2,1,1,3,18,5,1,1,6,30,8,1,1,9,42,11,1,1,12,54,14,1,1,15,77,17,1,1,18,78,20,1,1,21,90,\ldots]$](img72.png)
This suggests that after the initial 7, the 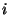 th group of 5
numbers is of the form
th group of 5
numbers is of the form
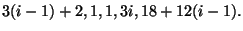
9i. We are looking for natural number solutions to
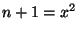 ,
,
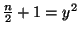 . Isolating
. Isolating 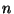 yields
yields
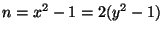 , implying that
, implying that
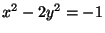 . There are
infinitely many solutions
. There are
infinitely many solutions 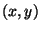 to this equation if the period
of the continued fraction of
to this equation if the period
of the continued fraction of 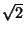 has odd order. Indeed,
has odd order. Indeed,
![$ \sqrt{2}=[1,\overline{2}]$](img82.png) . For each
. For each 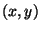 we can take
we can take
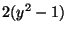 to find a unique (even)
to find a unique (even) 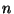 ; thus there are infinitely
many
; thus there are infinitely
many 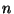 satisfying the desired property.
satisfying the desired property.
9ii. We can use the convergents program introduced in
class to produce a list of convergents for the continued fraction
of 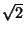 . The odd terms are of interest, and since we want
to find
. The odd terms are of interest, and since we want
to find 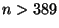 , we want the denominator of the convergent to be
at least 14. The first two such convergents are
, we want the denominator of the convergent to be
at least 14. The first two such convergents are
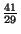 and
and
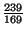 . They yield
. They yield
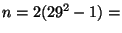 1680
and
1680
and
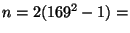 57120.
57120.
10. If 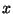 and
and 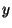 are consecutive integers, then we
have
are consecutive integers, then we
have
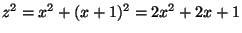 . Multiplying by 2, we have
. Multiplying by 2, we have
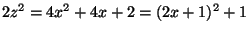 . Put
. Put 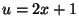 ; then
; then
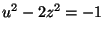 .
From the previous problem we know there are infinitely many
solutions to this equation for
.
From the previous problem we know there are infinitely many
solutions to this equation for 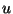 and
and 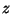 . Clearly each
solution
. Clearly each
solution 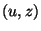 gives a unique
gives a unique 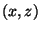 . Lastly we verify that
each of these solutions
. Lastly we verify that
each of these solutions 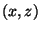 leads to a primitive Pythagorean
triple. But this is trivial: clearly
leads to a primitive Pythagorean
triple. But this is trivial: clearly 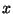 and
and 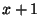 are coprime,
and if either shares a nontrivial divisor with
are coprime,
and if either shares a nontrivial divisor with 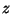 then the third
must also share this divisor, implying that
then the third
must also share this divisor, implying that 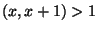 , which is
impossible.
, which is
impossible.



Next: About this document ...
William A Stein
2001-12-10