


Next: RSA Challenge
Up: Lecture 10: Attacking RSA
Previous: When and Are Close
Suppose that we crack an RSA cryptosystem by
finding a 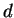 such that
for all
such that
for all 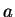 . Then we've found an
. Then we've found an 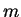 (
(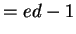 ) such that
) such that
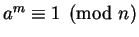 for all
for all 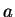 with
with
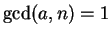 .
Knowing
.
Knowing 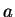 does not lead to a factorization of
does not lead to a factorization of 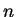 in as direct a manner as knowing
in as direct a manner as knowing
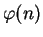 does (see
Section 1). However, there is a probabilistic
procedure that, given an
does (see
Section 1). However, there is a probabilistic
procedure that, given an 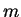 such that
such that
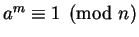 ,
will with high probability find a factorization of
,
will with high probability find a factorization of 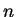 .
.
Probabilistic procedure to factor 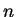 :
:
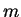 is even since
is even since
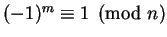 .
.
- If
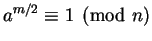 for all
for all 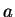 coprime to
coprime to 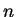 ,
replace
,
replace 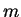 by
by 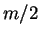 . In practice, it is not possible to determine
whether or not this condition holds, because it would require doing a
computation for too many
. In practice, it is not possible to determine
whether or not this condition holds, because it would require doing a
computation for too many 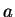 . Instead, we try a few random
. Instead, we try a few random 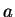 ; if
; if
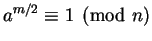 for the
for the 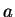 we check, then we divide
we check, then we divide 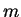 by
by 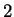 . (If there exists even a single
. (If there exists even a single 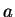 such that
such that
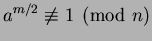 , then at least half the
, then at least half the 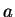 have this property.)
have this property.)
Keep repeating this step until we find an 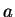 such that
such that
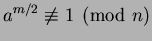 .
.
- There is a 50% chance that a randomly chosen
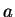 will have the property that
or
If the first case occurs, then
will have the property that
or
If the first case occurs, then
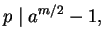
but
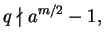
so
and we have factored 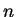 .
Just keep trying
.
Just keep trying 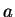 's until one of the cases occurs.
's until one of the cases occurs.
? \r rsa \\ load the file rsa.gp, available at Lecture 9 web page.
? rsa = make_rsa_key(10)
%34 = [32295194023343, 29468811804857, 11127763319273]
? n = rsa[1]; e = rsa[2]; d = rsa[3];
? m = e*d-1
%38 = 327921963064646896263108960
? for(a=2,20, if(Mod(a,n)^m!=1,print(a))) \\ prints nothing...
? m = m/2
%39 = 163960981532323448131554480
? for(a=2,20, if(Mod(a,n)^m!=1,print(a)))
? m = m/2
%40 = 81980490766161724065777240
? for(a=2,20, if(Mod(a,n)^m!=1,print(a)))
? m = m/2
%41 = 40990245383080862032888620
? for(a=2,20, if(Mod(a,n)^m!=1,print(a)))
? m = m/2
%42 = 20495122691540431016444310
? for(a=2,20,if(Mod(a,n)^m!=1,print(a)))
2
5
6
... etc.
? gcd(2^m,n)
*** power overflow in pow_monome.
? x = lift(Mod(2,n)^m)-1
%43 = 4015382800098
? gcd(x,n)
%46 = 737531
? p = gcd(x,n)
%53 = 737531
? q = n/p
? p*q
%54 = 32295194023343
? n
%55 = 32295194023343



Next: RSA Challenge
Up: Lecture 10: Attacking RSA
Previous: When and Are Close
William A Stein
2001-10-04
![]() :
:
![]() such that
such that
![]() .
.