


Next: Numbers Do Factor
Up: Greatest Common Divisors
Previous: Greatest Common Divisors
Can we easily compute something like
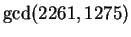 ? Yep.
Watch closely:
Notice that if a number
? Yep.
Watch closely:
Notice that if a number 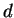 divides both
divides both 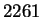 and
and 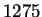 , then it
automatically divides
, then it
automatically divides 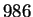 , and of course
, and of course 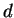 divides
divides 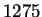 . Also, if a number
divides both
. Also, if a number
divides both 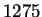 and
and 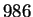 , then it has got to divide
, then it has got to divide 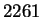 as well!
So we have made progress:
Let's try again:
so
as well!
So we have made progress:
Let's try again:
so
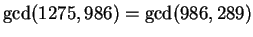 .
Just keep at it:
.
Just keep at it:
Thus
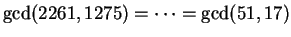 , which is
, which is 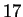 because
because 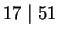 , so
Cool. Aside from tedious arithmetic, that was
quick and very mechanical.
, so
Cool. Aside from tedious arithmetic, that was
quick and very mechanical.
The Algorithm:
That was an illustration of Euclid's algorithm.
You just ``Divide and switch.''
More formally, fix
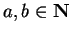 with
with 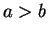 .
Using ``divide with quotient and remainder'',
write
.
Using ``divide with quotient and remainder'',
write 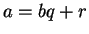 , with
, with 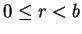 .
Then, just as above,
.
Then, just as above,
Let 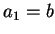 ,
, 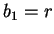 , and repeat until
, and repeat until 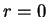 .
Soon enough we have computed
.
Soon enough we have computed 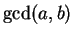 .
.
Here's are two more examples:
Example 2.2
Set
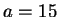
and
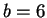
.
We can just as easily do an example that is ``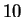 times as hard'':
times as hard'':
Example 2.3
Set
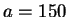
and
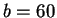
.
With Euclid's algorithm in hand, we can prove that if a prime divides the
product of two numbers, then it has got to divide one of them. This
result is the key to proving that prime factorization
is unique.
Proof.
If
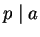
we are done. If
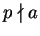
then
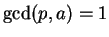
, since
only
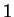
and
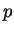
divide
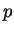
. Stepping through the Euclidean algorithm
from above, we see that
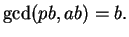
At each step, we simply
multiply the equation through by
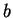
. Since
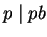
and,
by hypothesis,
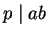
, it follows that
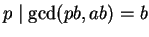
.




Next: Numbers Do Factor
Up: Greatest Common Divisors
Previous: Greatest Common Divisors
William A Stein
2001-09-14
![]() with
with ![]() .
Using ``divide with quotient and remainder'',
write
.
Using ``divide with quotient and remainder'',
write ![]() , with
, with ![]() .
Then, just as above,
.
Then, just as above,