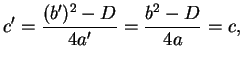There is a geometric interpretation of reduced, which we will not
use this later. Let
![]() and set
and set
![]() , so
, so ![]() is the root of
is the root of
![]() with positive imaginary part. The right action of
with positive imaginary part. The right action of
![]() on
positive definite binary quadratic forms corresponds to the left
action of
on
positive definite binary quadratic forms corresponds to the left
action of
![]() by linear fractional transformations on the
complex upper half plane
by linear fractional transformations on the
complex upper half plane
![]() Im
Im![]() . The standard
fundamental domain for the action of
. The standard
fundamental domain for the action of
![]() on
on
![]() is
is
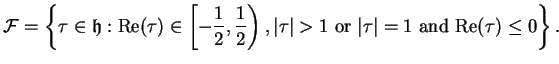
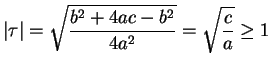
The following theorem (which is not proved in Davenport) highlights the importance of reduced forms.
We first prove that there is a reduced form in every class.
Let
![]() be an equivalence class of positive definite
quadratic forms of discriminant
be an equivalence class of positive definite
quadratic forms of discriminant ![]() . Let
. Let ![]() be
an element of
be
an element of
![]() such that
such that ![]() is minimal (amongst elements
of
is minimal (amongst elements
of
![]() ). Note that for any such form we
have
). Note that for any such form we
have ![]() , since
, since ![]() is equivalent to
is equivalent to
![]() (use the matrix
(use the matrix
![]() ).
Applying the element
).
Applying the element
![]() to
to ![]() for a suitably chosen integer
for a suitably chosen integer ![]() (precisely,
(precisely,
![]() ) results in a form
) results in a form
![]() with
with ![]() and
and
![]() .
Since
.
Since ![]() is minimal, we have just as above that
is minimal, we have just as above that
![]() , hence
, hence
![]() is ``just about'' reduced.
The only possible remaining problem would occur if
is ``just about'' reduced.
The only possible remaining problem would occur if ![]() and
and ![]() . In that case, changing
. In that case, changing
![]() to
to
![]() results in an equivalent form with
results in an equivalent form with ![]() , so that
, so that
![]() is reduced.
is reduced.
Next suppose ![]() is a reduced form. We
will now establish that
is a reduced form. We
will now establish that ![]() is the only reduced form
in its equivalence class. First, we check that
is the only reduced form
in its equivalence class. First, we check that ![]() is minimal amongst all
forms equivalent to
is minimal amongst all
forms equivalent to ![]() . Indeed, every other
. Indeed, every other ![]() has the
form
has the
form
![]() with
with ![]() coprime integers (see this
by hitting
coprime integers (see this
by hitting ![]() by
by
![]() ). The
identities
). The
identities
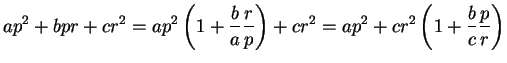
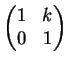 (corresponding
to
(corresponding
to