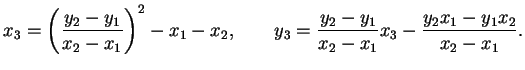Next: To Infinity!
Up: Lecture 25: Elliptic Curves
Previous: Linear and Quadratic Diophantine
Next suppose that  is an irreducible cubic polynomial.
The question of whether or not
is an irreducible cubic polynomial.
The question of whether or not  has a rational solution is
still an open problem! We will not consider this problem
further until we discuss the Birch and Swinnerton-Dyer conjecture.
has a rational solution is
still an open problem! We will not consider this problem
further until we discuss the Birch and Swinnerton-Dyer conjecture.
Suppose that  has a given rational solution. Then one can change
coordinates so that the question of finding the rational solutions to
has a given rational solution. Then one can change
coordinates so that the question of finding the rational solutions to
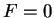 is equivalent to the problem of finding all rational points on
the elliptic curve
is equivalent to the problem of finding all rational points on
the elliptic curve
Recall that when 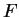 has degree
has degree 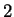 we can use a given rational
point
we can use a given rational
point 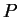 on the graph of
on the graph of 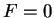 to find all other rational points by
intersecting a line through
to find all other rational points by
intersecting a line through 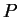 with the graph of
with the graph of 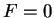 .
The graph of
.
The graph of
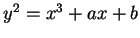 looks like
looks like
[egg and curvy line] or [curvier line]
Notice that if 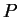 is a point on the graph of the curve, then a line
through
is a point on the graph of the curve, then a line
through 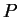 (usually) intersects the graph in exactly two other
points. In general, these two other points usually do not have
rational coordinates. However, if
(usually) intersects the graph in exactly two other
points. In general, these two other points usually do not have
rational coordinates. However, if 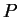 and
and 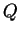 are rational points on
the graph of
are rational points on
the graph of
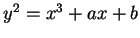 and
and 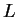 is the line through
is the line through 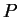 and
and 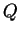 ,
then the third point of intersection with the graph will have rational
coordinates. Explicitly, if
,
then the third point of intersection with the graph will have rational
coordinates. Explicitly, if
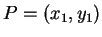 and
and
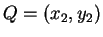 then the
third point of intersection has coordinates1
Thus, given two points on
then the
third point of intersection has coordinates1
Thus, given two points on 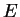 , we can find another. Also, given a single
point, we can draw the tangent line to
, we can find another. Also, given a single
point, we can draw the tangent line to 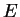 through that point and obtain
a third point.
through that point and obtain
a third point.
Subsections



Next: To Infinity!
Up: Lecture 25: Elliptic Curves
Previous: Linear and Quadratic Diophantine
William A Stein
2001-11-09
![]() has a given rational solution. Then one can change
coordinates so that the question of finding the rational solutions to
has a given rational solution. Then one can change
coordinates so that the question of finding the rational solutions to
![]() is equivalent to the problem of finding all rational points on
the elliptic curve
is equivalent to the problem of finding all rational points on
the elliptic curve
![]() has degree
has degree ![]() we can use a given rational
point
we can use a given rational
point ![]() on the graph of
on the graph of ![]() to find all other rational points by
intersecting a line through
to find all other rational points by
intersecting a line through ![]() with the graph of
with the graph of ![]() .
The graph of
.
The graph of
![]() looks like
looks like