


Next: Nikita and Michael
Up: Microsoft Digital Rights Management
Previous: Microsoft Digital Rights Management
The elliptic curve used in MS-DRM is an elliptic curve over the finite
field
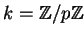 , where
As Beale Screamer remarks, this modulus has high nerd appeal because in
hexadecimal it is
, where
As Beale Screamer remarks, this modulus has high nerd appeal because in
hexadecimal it is
89ABCDEF012345672718281831415926141424F7,
which
includes counting in hexadecimal, and digits of 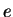 ,
,
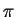 , and
, and 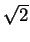 .
The Microsoft elliptic curve
.
The Microsoft elliptic curve 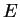 is
is
We have
and the group 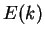 is cyclic with generator
is cyclic with generator
William A Stein
2001-11-20