


Next: Some Tools for Computing
Up: Lecture 3: Introduction to
Previous: Introduction
A computer can quickly ``convince'' you that many assertions
about prime numbers are true. Here are three.
- The polynomial
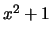 takes on infinitely many prime values.
takes on infinitely many prime values.
Let
With a computer, we quickly find that
Surely 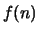 is unbounded!
The PARI code to compute
is unbounded!
The PARI code to compute 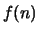 is very simple:
is very simple:
? f(n) = s=0; for(x=1,n,if(isprime(x^2+1),s++)); s
? f(100)
%1 = 19
? f(1000)
%2 = 112
? f(10000)
%3 = 841
? f(100000)
%4 = 6656
- Every even integer
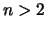 is a sum of two primes.
is a sum of two primes.
With a computer we find that this seems true
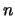 |
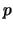 |
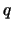 |
| 4 |
2 |
2 |
| 6 |
3 |
3 |
| 8 |
3 |
5 |
| 10 |
3 |
7 |
| 12 |
5 |
7 |
... and much further. In practice, it's easy to write
an even number as a sum of two primes. Why should there
be any weird even numbers out there for which this can't be done?
PARI code to find 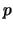 and
and 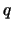 :
:
? gb(n) = forprime(p=2,n,if(isprime(n-p),return([p,n-p])));
? gb(4)
%7 = [2, 2]
? gb(6)
%8 = [3, 3]
? gb(100)
%9 = [3, 97]
? gb(1000)
%10 = [3, 997]
? gb(570) \\ takes no time at all!
%11 = [7, 563]
- There are infinitely many primes
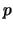 such that
such that 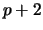 is also prime.
is also prime.
Let
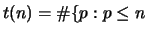 and
and 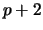 is prime
is prime 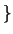 .
Using a computer we quickly find that
The PARI code to compute
.
Using a computer we quickly find that
The PARI code to compute 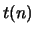 is very simple:
is very simple:
? t(n) = s=0; forprime(p=2,n,if(isprime(p+2),s++)); s
? t(10^2)
%12 = 8
? t(10^3)
%13 = 35
? t(10^4)
%14 = 205
? t(10^5)
%15 = 1224
Surely 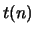 keeps getting bigger!!
keeps getting bigger!!
As it turns out, these three assertions are all OLD famous
extremely difficult unsolved problems! Anyone who proves
one of them will be very famous.
Assertion 2 is called ``The Goldbach Conjecture'';
Goldbach reformulated it in a letter to Euler in 1742. It's
featured in the following recent novel:
The publisher of that novel offers a MILLION dollar prize
for the solution to the Goldbach conjecture:
http://www.faber.co.uk/faber/million_dollar.asp?PGE=&ORD=faber&TAG=&CID=
The Goldbach conjecture is true for all
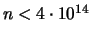 , see
, see
http://www.informatik.uni-giessen.de/staff/richstein/ca/Goldbach.html
Assertion 3 is the ``Twin Primes Conjecture''. According to
http://perso.wanadoo.fr/yves.gallot/primes/chrrcds.html#twin
on May 17, 2001, David Underbakke and Phil Carmody discovered
a 32220 digits twin primes record with a set of different
programs:
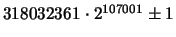 . This is the current
``world record''.
. This is the current
``world record''.
With a computer, even if you can't solve one of these ``Grand
Challenge'' problems, at least you can perhaps work very hard and
prove it for more cases than anybody before you, especially since
computers keep getting more powerful. This can be very fun,
especially as you search for a more efficient algorithm to extend the
computations.



Next: Some Tools for Computing
Up: Lecture 3: Introduction to
Previous: Introduction
William A Stein
2001-09-17
