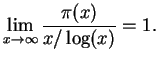Next: Counting Primes Today
Up: Lecture 4: The Sequence
Previous: Primes of the form
There are infinitely many primes.
Can we say something more precise?
Let's consider a similar question:
Question 3.1
How many even integers are there?
Answer: Half of all integers.
Question 3.2
How many integers are there of the form
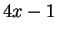
?
Answer: One fourth of all integers.
Question 3.3
How many perfect squares are there?
Answer: Zero percent of all numbers, in the sense that
the limit of the proportion of perfect squares to all numbers
converges to 0.
More precisely,
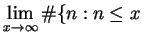
and $n$ is a perfect square
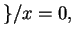
since the numerator is roughly 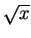 and
and
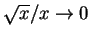 .
.
A better question is:
Question 3.4
How many numbers
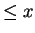
are perfect squares, as a function of
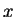
?
Answer: Asymptotically, the answer is 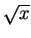 .
.
So a good question is:
Question 3.5
How many numbers
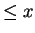
are prime?
Let
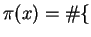
primes
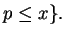
For example,
We can compute a few more values of 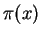 using PARI:
using PARI:
? pi(x, c=0) = forprime(p=2,x,c++); c;
? for(n=1,7,print(n*100,"\t",pi(n*100)))
100 25
200 46
300 62
400 78
500 95
600 109
700 125
Now draw a graph on the blackboard. It will look like a straight
line...
Gauss spent some of his free time counting primes. By the end
of his life, he had computed 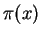 for
for 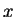 up to
up to 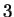 million.
million.
(I don't know if Gauss got the right answer.)
Gauss conjectured the following:
Theorem 3.6 (Hadamard, Vallée Poussin, 1896)
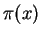
is asymptotic to
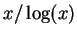
, in the sense that
I will not prove this theorem in this class.
The theorem implies that
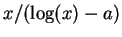 can be used
to approximate
can be used
to approximate 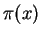 , for any
, for any 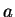 . In fact,
. In fact, 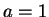 is the best choice.
is the best choice.
? pi(x, c=0) = forprime(p=2,x,c++); c;
? for(n=1,10,print(n*1000,"\t",pi(n*1000),"\t",n*1000/(log(n*1000)-1)))
1000 168 169.2690290604408165186256278
2000 303 302.9888734545463878029800994
3000 430 428.1819317975237043747385740
4000 550 548.3922097278253264133400985
5000 669 665.1418784486502172369455815
6000 783 779.2698885854778626863677374
7000 900 891.3035657223339974352567759
8000 1007 1001.602962794770080754784281
9000 1117 1110.428422963188172310675011
10000 1229 1217.976301461550279200775705
Remark 3.7
Subsections



Next: Counting Primes Today
Up: Lecture 4: The Sequence
Previous: Primes of the form
William A Stein
2001-09-19
![]() using PARI:
using PARI:
![]() for
for ![]() up to
up to ![]() million.
million.