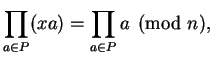Fermat's Little Theorem

Definition 4.1 (Order)   Let $n\in\mathbb{N}$ and $x\in\mathbb{Z}$ with $\gcd(x,n)=1$. The order of $x$ modulo $n$ is the smallest $m\in\mathbb{N}$ such that

$$x^m \equiv 1\pmod{n}.$$

We must show that this definition makes sense. To do so, we verify that such an $m$ exists. Consider $x, x^2, x^3, \ldots$ modulo $n$. There are only finitely many residue classes modulo $n$, so we must eventually find two integers $i, j$ with $i<j$ such that

$$x^i\equiv x^j\pmod{n}.$$

Since $\gcd(x,n)=1$, Proposition 2.1 implies that we can cancel $x$'s and conclude that

$$x^{j-i}\equiv 1\pmod{n}.$$

Definition 4.2 (Euler Phi function)   Let

$$\varphi (n) = \char93 \{a \in \mathbb{N}: a \leq n$$    and $$\gcd(a,n)=1\}.$$

For example,

$$\varphi (1) = \char93 \{1\} = 1,$$

$$\varphi (5) = \char93 \{1,2,3,4\} = 4,$$

$$\varphi (12) = \char93 \{1,5,7,11\} = 4.$$

If $p$ is any prime number then

$$\varphi (p) = \char93 \{1,2,\ldots,p-1\} = p-1.$$

Theorem 4.3 (Fermat's Little Theorem)   If $\gcd(x,n)=1$, then

$$x^{\varphi (n)} \equiv 1\pmod{n}.$$

Proof. Let

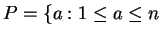
$$P = \{ a : 1\leq a \leq n$$    and $$\gcd(a,n)=1\}.$$

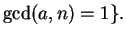
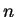
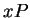
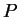
In the same way that we proved Lemma 3.2, we see that the reductions modulo $n$ of the elements of $xP$ are exactly the same as the reductions of the elements of $P$. Thus

$$\prod_{a\in P} (xa) = \prod_{a \in P} a \pmod{n},$$

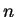
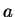
since the products are over exactly the same numbers modulo $n$. Now cancel the $a$'s on both sides to get

$$x^{\char93 P} \equiv 1\pmod{n},$$

as claimed. $\qedsymbol$