


Next: Some Quotes
Up: Lecture 8: Public-key Crypto
Previous: Public-key Cryptography
Nikita and Michael agree on a prime number 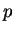 and
an integer
and
an integer 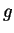 that has order
that has order 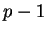 modulo
modulo 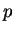 .
(So
.
(So
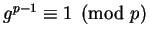 , but
, but
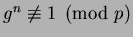 for any positive
for any positive 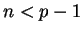 .) Nikita chooses a random number
.) Nikita chooses a random number
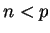 , and Michael chooses a random number
, and Michael chooses a random number 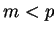 .
Nikita sends
.
Nikita sends
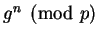 to Michael, and Michael
sends
to Michael, and Michael
sends
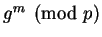 to Nikita.
Nikita can now compute the secret key:
Likewise, Michael computes the secret key:
Now Nikita uses the secret key
to Nikita.
Nikita can now compute the secret key:
Likewise, Michael computes the secret key:
Now Nikita uses the secret key 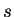 to send Michael
an encrypted version of her critical message. Michael,
who also knows
to send Michael
an encrypted version of her critical message. Michael,
who also knows 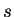 , is able to decode the message.
, is able to decode the message.
Meanwhile, hackers in The Collective see both
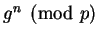 and
and
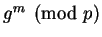 , but they aren't able to use this information to deduce
either
, but they aren't able to use this information to deduce
either 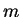 ,
, 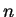 , or
, or
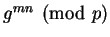 quickly enough to stop Michael
from thwarting their plans. Yeah!
quickly enough to stop Michael
from thwarting their plans. Yeah!
The Diffie-Hellman key exchange is the first public-key cryptosystem
every published (1976). The system was discovered by GCHQ (British
intelligence) a few years before Diffie and Hellman found it, but they
couldn't tell anyone about their work; perhaps it was discovered by
others before. That this system was discovered independently more
than once shouldn't surprise you, given how simple it is!
Subsections



Next: Some Quotes
Up: Lecture 8: Public-key Crypto
Previous: Public-key Cryptography
William A Stein
2001-09-28
![]() and
and
![]() , but they aren't able to use this information to deduce
either
, but they aren't able to use this information to deduce
either ![]() ,
, ![]() , or
, or
![]() quickly enough to stop Michael
from thwarting their plans. Yeah!
quickly enough to stop Michael
from thwarting their plans. Yeah!