Math 480 (Spring 2007): Homework 3
Due: Monday, April 16
There are 8 problems. Each problem is worth 6 points
and parts of multipart problems are worth equal amounts.
- Let
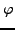 be the Euler phi function. The first few values
of
be the Euler phi function. The first few values
of 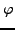 are as follows (you do not have to prove this):
are as follows (you do not have to prove this):
1 1 2 2 4 2 6 4 6 4 10 4 12 6 8 8 16 6 18 8 12 10 22 8 20 12 18 12 28
Notice that most of these numbers are even.
Prove for all 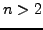 that
that
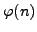 is an even integer.
(You may using anything that is proved
about
is an even integer.
(You may using anything that is proved
about 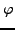 in the course textbook.)
in the course textbook.)
- Compute each of the following entirely by hand - no calculator.
In each case, given the problem
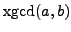 ,
your final answer will be integers
,
your final answer will be integers 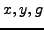 such that
such that
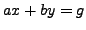 . It is probably best to use the algorithm
I described in class, which is also in the newest version
of the course notes.
. It is probably best to use the algorithm
I described in class, which is also in the newest version
of the course notes.
-
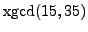
-
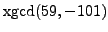
-
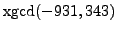
-
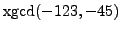
-
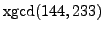
- Find integers
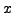 and
and 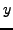 such that
such that
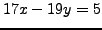 .
.
- Do each of the following using any means (including a computer).
As in the previous problem, your answer is integers
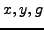 such
that
such
that 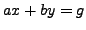 .
.
-
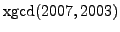
-
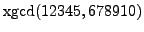
-
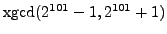
- Prove that there are infinitely many composite numbers
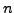 such that for all
such that for all 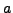 with
with
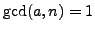 , we have
, we have
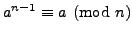 . (Hint: consider
. (Hint: consider 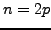 with
with 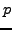 an odd prime.)
an odd prime.)
- Solve each of the following equations for
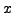 (you may use a computer
if necessary):
(you may use a computer
if necessary):
-
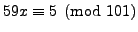
-
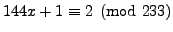
-
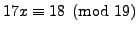
- Prime numbers
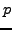 and
and 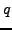 are called twin primes if
are called twin primes if 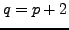 .
For example, the first few twin prime pairs are
.
For example, the first few twin prime pairs are
and it is an open problem to prove that there are infinitely many.
Notice in the above list of pairs 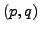 that, except for the first pair,
we have that
that, except for the first pair,
we have that 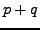 is divisible by
is divisible by 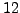 .
Prove that if
.
Prove that if 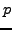 and
and 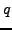 are twin primes with
are twin primes with 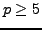 ,
then
,
then
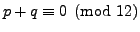 , as follows:
, as follows:
- Prove that if
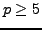 is prime, then
is prime, then
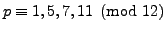 ,
i.e., there are only four possibilities for
,
i.e., there are only four possibilities for 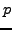 modulo
modulo 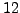 .
.
- Show that if
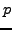 and
and 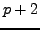 are both prime with
are both prime with 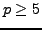 , then
, then
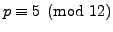 or
or
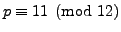 .
.
- Conclude that
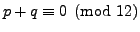 .
.
- Let
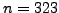 . Do the following by hand:
. Do the following by hand:
- Write
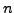 in binary, i.e., base
in binary, i.e., base 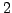 .
.
- Compute
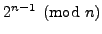 by hand.
by hand.
- Is
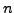 prime. Why or why not?
prime. Why or why not?
- Let
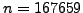 .
.
- Use a computer to write
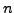 in binary.
E.g., in SAGE, use 167659.str(2).
in binary.
E.g., in SAGE, use 167659.str(2).
- Use a computer to compute
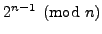 , e.g.,
in SAGE do
, e.g.,
in SAGE do n=167659; Mod(2,n)^(n-1).
- Is
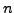 prime?
prime?
William
2007-04-11