Math 480 (Spring 2007): Homework 7
Due: Monday, May 14
There are 6 exciting problems. Each problem is worth 6 points
and parts of multipart problems are worth equal amounts. You may work
with other people and use a computer, unless otherwise stated. Acknowledge
those who help you.
- Find a continued fraction that equals each
of the following rational numbers:
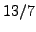
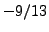
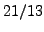
- Find the value (which is a rational number)
of each of the following continued fractions.
![$ [1,2,3]$](img4.png)
![$ [0,1,5,2]$](img5.png)
![$ [3,7,15]$](img6.png)
- Let
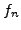 be the
be the 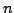 th Fibonacci number, so
th Fibonacci number, so 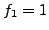 ,
,
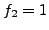 , and for
, and for 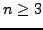 we have
we have
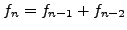 .
Prove that the continued fraction expansion of
.
Prove that the continued fraction expansion of
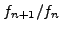 consists of
consists of 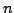
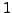 's, i.e.,
's, i.e.,
- Prove that if
![$ [a_0\ldots, a_n]$](img16.png) and
and
![$ [b_0,\ldots b_m]$](img17.png) are two simple continued fractions that have the same value,
and that
are two simple continued fractions that have the same value,
and that
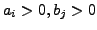 for all
for all 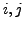 ,
and
,
and 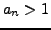 and
and 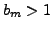 , then
, then 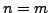 and
and 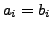 for
all
for
all 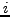 . Thus the continued fraction expansion
of a rational number is unique if the last term is
required to be larger than
. Thus the continued fraction expansion
of a rational number is unique if the last term is
required to be larger than 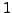 .
.
- Show how to use continued fractions
to find a rational number
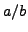 in lowest terms such that
in lowest terms such that
- The number
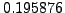 is a decimal approximation to a rational
number
is a decimal approximation to a rational
number 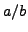 with
with 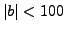 . Show how to use
continued fractions to find
. Show how to use
continued fractions to find 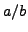 .
.
William
2007-05-09
![$\displaystyle \frac{f_{n+1}}{f_{n}} = [1,1,\ldots, 1].
$](img15.png)
![$\displaystyle \left\vert\frac{a}{b} - \sqrt[3]{2}\right\vert < \frac{1}{b^2} < 0.001.$](img26.png)