William Stein
Date: Math 124 ![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001
Second proof (using continued fractions): Consider the periodic
continued fraction
![]() . The
. The ![]() th convergent to this
continued fraction is
th convergent to this
continued fraction is ![]() , where
, where ![]() and
and ![]() are defined by
the recurrence
are defined by
the recurrence
![]() ,
,
![]() , and
, and
![]() ,
, ![]() ,
, ![]() . As observed in Lecture 17,
. As observed in Lecture 17,
![]() . Now just notice that
. Now just notice that
![]() and
and
![]() .
.
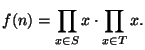
Thus the group ![]() is isomorphic to the
is isomorphic to the
![]() -vector space
-vector space
![]() , where again
, where again ![]() is the number of prime factors of
is the number of prime factors of ![]() . By a
careful induction we see that
. By a
careful induction we see that
![]() if and only
if
if and only
if ![]() . To see this, check the cases
. To see this, check the cases ![]() directly. For
directly. For ![]() , write
, write
![]() as a union of two
as a union of two ![]() -dimensional hyperplanes, the
elements of each of which sum to 0, by the inductive hypothesis.
Thus
-dimensional hyperplanes, the
elements of each of which sum to 0, by the inductive hypothesis.
Thus
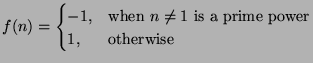
f(n)=local(s);s=1;for(x=1,n,if(gcd(x,n)==1,s=(s*x)%n));return(s);
In Lecture 11, we proved that the group
![]() of order
of order ![]() is cyclic,
so since the homomorphism
is cyclic,
so since the homomorphism
![]() is surjective, there is an
is surjective, there is an
![]() of
order a multiple of
of
order a multiple of ![]() . Then
. Then
![]() has order
has order ![]() .
Next, letting
.
Next, letting ![]() , the binomial theorem implies that
, the binomial theorem implies that
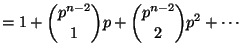 |
||
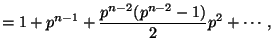 |
[If you're worried about that binomial expansion, the following
remark by ``A. Student'' might prove helpful: For ![]() we
have
we
have
![]() , because
, because
![]() and the power of
and the power of ![]() in the factorization of
in the factorization of ![]() satisfies
satisfies
![]() .]
.]
![$\displaystyle \alpha = [\overline{1,6,3,1}] =
1+\frac{1}{6+\frac{1}{3+\frac{1}{1+\frac{1}{\alpha}}}}.
$](img94.png)
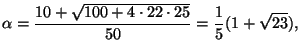
ss(n) = for(x=1,floor(sqrt(n)),if(issquare(n-x^2),print(x)))However, ss(m) will take an extraordinarily long time to terminate, so instead we use the proof that integers of a certain form are a sum of two squares. First, factor
? (4153+12410*I)*(14460+23441*I)*(17946+22261*I) %14 = -10304665980833 - 171525258172*IThus
? r=reducedforms(-888)
%2 = [[1, 0, 222], [11, -6, 21], [11, 6, 21], [13, -10, 19],
[13, 10, 19], [14, -8, 17], [14, 8, 17], [2, 0, 111],
[3, 0, 74], [6, 0, 37], [7, -6, 33], [7, 6, 33]]
Thus the class group has order ? for(n=1,12,print1(orderform(r[n],r[1])," ")) 1 6 6 6 6 6 6 2 2 2 3 3Since no element has order
? e = ellinit([0,-4,0,0,16]) ? forprime(p=3,30,if(p!=11,print1(p+1-ellap(e,p),", "))) 5, 5, 10, 10, 20, 20, 25, 30, \\ 3 5 7 13 17 19 23 29
? q*prod(n=1,30,(1-q^n)^2)*prod(n=1,3,(1-q^(11*n))^2) + O(q^30)
%22 = q - 2*q^2 - q^3 + 2*q^4 + q^5 + 2*q^6 - 2*q^7 - 2*q^9 - 2*q^10
+ q^11 - 2*q^12 + 4*q^13 + 4*q^14 - q^15 - 4*q^16 - 2*q^17
+ 4*q^18 + 2*q^20 + 2*q^21 - 2*q^22 - q^23 - 4*q^25 - 8*q^26
+ 5*q^27 - 4*q^28 + O(q^30)
? forprime(p=3,30,print1(p+1-ellap(e,p)," ")) 4 4 8 12 20 16 20 24 20
{ECM(N, m)= local(E);
E = ellinit([0,0,0,random(N),1]*Mod(1,N));
print("E: y^2 = x^3 + ",lift(E[4]),"x+1, P=[0,1]");
ellpow(E,[0,1]*Mod(1,N),m); \\ this fails if and only if we win!
}
{lcmfirst(B) =
local(L,i); L=1; for(i=2,B,L=lcm(L,i));
return(L);
}
I'm going to start with lcmfirst(10000), though you might
have choosen something different for ? m = lcmfirst(10000); ? N = 124531325385603661726997; ? ECM(N,m) E: y^2 = x^3 + 90450397866599611397131x+1, P=[0,1] *** impossible inverse modulo: Mod(495899, 124531325385603661726997).We have thus split
? ECM(N/495899,m) E: y^2 = x^3 + 35484437310832518x+1, P=[0,1] *** impossible inverse modulo: Mod(311221384171, 251122356337890703).Thus
? isprime(495899,1) %5 = 1 ? isprime(311221384171,1) %6 = 0 ? isprime(806893,1) %7 = 1
When we try ECM on the second factor, it fails a few times, then succeeds:
? ECM(311221384171,m) E: y^2 = x^3 + 246181556758x+1, P=[0,1] %8 = [0] ? ECM(311221384171,m) E: y^2 = x^3 + 163571326944x+1, P=[0,1] %9 = [Mod(20641240315, 311221384171), Mod(200682828122, 311221384171)] ? ECM(311221384171,m) E: y^2 = x^3 + 255080864418x+1, P=[0,1] *** impossible inverse modulo: Mod(888161, 311221384171).Thus
? factor(N) %11 = [350411 1] [495899 1] [806893 1] [888161 1]