



Next: Computing in The Group
Up: Lecture 28: Computing with
Previous: Contents
Contents
We are concerned primarily with elliptic curves
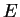 given by an equation of the form
with
given by an equation of the form
with 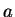 and
and 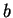 either rational
numbers or elements of a finite field
either rational
numbers or elements of a finite field
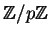 . If
. If 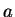 and
and 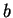 are
in
are
in
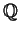 , we initialize
, we initialize 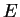 in PARI using the following command:
in PARI using the following command:
? E = ellinit([0,0,0,a,b]);
If you wish to view 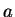 and
and 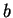 as element of
as element of
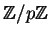 , initialize
, initialize 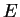 as follows:
as follows:
? E = ellinit([0,0,0,a,b]*Mod(1,p));
If
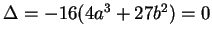 then
ellinit will complain; otherwise, ellinit returns
a
then
ellinit will complain; otherwise, ellinit returns
a 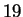 -component vector of information about
-component vector of information about 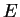 . You can
access some of this information using the
dot notation, as shown below.
. You can
access some of this information using the
dot notation, as shown below.
? E = ellinit([0,0,0,1,1]);
? E.a4
%11 = 1
? E.a6
%12 = 1
? E.disc
%13 = -496
? E.j
%14 = 6912/31
? E5 = ellinit([0,0,0,1,1]*Mod(1,5));
? E5.disc
%15 = Mod(4, 5)
? E5.j
%16 = Mod(2, 5)
Here E.j is the 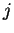 -invariant of
-invariant of 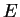 . It is
equal to
. It is
equal to
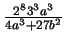 ,
and has some remarkable properties that I probably
won't tell you about.
,
and has some remarkable properties that I probably
won't tell you about.
Most elliptic curves functions in PARI take as their first argument
the output of ellinit. For example, the function
ellisoncurve(E,P) takes the output of ellinit as its
first argument and a point P=[x,y], and returns 1 if P
lies on E and 0 otherwise.
? P = [0,1]
? ellisoncurve(E, P)
%17 = 1
? P5 = [0,1]*Mod(1,5)
? ellisoncurve(E5, P)
%18 = 1
William A Stein
2001-11-21