A Rationality Theorem

In the last lecture, I mentioned that it is incredibly difficult to say anything precise about $L(E,s)$, even with the above formulas. For example, it is a very deep theorem (Gross-Zagier) that there is an elliptic curve such that

$$L(E,s) = c(s-1)^3 +$$    higher terms$$,$$

and nobody has any idea how to prove that there is an elliptic curve with

$$L(E,s) = c(s-1)^4 +$$    higher terms$$.$$

Fortunately, it is possible to decide whether or not $L(E,1)=0$.

Theorem 4.1   Let $y^2 = x^3 + ax + b$ be an elliptic curve. Let

$$\Omega_E = \int_{\gamma}^{\infty} \frac{dx}{\sqrt{x^3+ax+b}},$$

where $\gamma$ is the largest real root of $x^3 +ax+b$. Then

$$\frac{L(E,1)}{\Omega_E} \in \mathbb{Q}$$

and it is straightforward in any particular case to bound the denominator of that rational number.

In practice, one computes this integral using the ``Arithmetic-Geometric Mean''. In PARI, $\Omega_E$ is approximated by E.omega[1] (times a small power of $2$).

Example 4.2   Let $E$ be the elliptic curve $y^2 = x^3 - 43x + 166$. We compute $L(E,1)$ using the above formula and observe that $L(E,1)/\Omega_E$ appears to be a rational number, as predicted by the theorem.

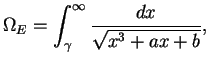
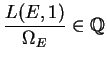
? E = ellinit([0,0,0,-43,166]);
? E = ellchangecurve(E, ellglobalred(E)[2]);
? eps = ellrootno(E)
%77 = 1
? N = ellglobalred(E)[1]
%78 = 26
? L = (1+eps) * sum(n=1,100, ellak(E,n)/n * exp(-2*Pi*n/sqrt(N)))
%79 = 0.6209653495490554663758626727
? Om = E.omega[1]
%80 = 4.346757446843388264631038710
? L/Om
%81 = 0.1428571428571428571428571427
? contfrac(L/Om)
%84 = [0, 7]
? 1/7.0
%85 = 0.1428571428571428571428571428
? elltors(E)
%86 = [7, [7], [[1, 0]]]

Notice that in this example, $L(E,1)/\Omega_E = 1/7 = 1/\char93 E(\mathbb{Q})$. This is shadow of a more refined conjecture of Birch and Swinnerton-Dyer.

Monday's lecture will be filled with numerical examples and numerical evidence for the Birch and Swinnerton-Dyer conjecture. Wednesday's lecture will be a review for the take-home FINAL EXAM.