Next: Areas in Polar Coordinates Up: Polar Coordinates and Complex Previous: Polar Coordinates and Complex Contents Index
Polar coordinates are extremely useful, especially
when thinking about complex numbers. Note, however,
that the
![]() representation of a point is
very non-unique.
representation of a point is
very non-unique.
First, ![]() is not determined by the point. You could add
is not determined by the point. You could add ![]() to it and get the same point:
to it and get the same point:
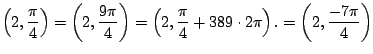
Also that ![]() can be negative introduces further non-uniqueness:
can be negative introduces further non-uniqueness:
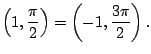
We can convert back and forth between cartesian and polar coordinates using that
| (4.1) | ||
| (4.2) |
| (4.3) | ||
| (4.4) |
We plug in points for one period of the function we are
graphing--in this case ![]() :
:
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
To more accurately draw the graph, let's try converting the equation to
one involving polar coordinates. This is easier if we multiply both
sides by ![]() :
:
Actually any polar graph of the form
![]() is a circle, as you will see in homework problem 67
by generalizing what we just did.
is a circle, as you will see in homework problem 67
by generalizing what we just did.
William Stein 2006-03-15