Next: Finishing the proof of Up: Dirichlet's Unit Theorem Previous: Dirichlet's Unit Theorem Contents Index
We prove the theorem by defining a map
![]() , and
showing that the kernel of
, and
showing that the kernel of ![]() is finite and the image of
is finite and the image of ![]() is a lattice in a hyperplane in
is a lattice in a hyperplane in
![]() . The trickiest part of the
proof is showing that the image of
. The trickiest part of the
proof is showing that the image of ![]() spans a hyperplane, and we
do this by a clever application of Blichfeldt's lemma (that if
spans a hyperplane, and we
do this by a clever application of Blichfeldt's lemma (that if ![]() is
closed, bounded, symmetric, etc., and has volume at least
is
closed, bounded, symmetric, etc., and has volume at least
![]() , then
, then ![]() contains a nonzero element).
contains a nonzero element).
He is a rather tall, lanky-looking man, with moustache and beard about to turn grey with a somewhat harsh voice and rather deaf. He was unwashed, with his cup of coffee and cigar. One of his failings is forgetting time, he pulls his watch out, finds it past three, and runs out without even finishing the sentence.Koch wrote that:
... important parts of mathematics were influenced by Dirichlet. His proofs characteristically started with surprisingly simple observations, followed by extremely sharp analysis of the remaining problem.I think Koch's observation nicely describes the proof we will give of Theorem 12.1.2.
The following proposition explains how to think about units in terms of the norm.
Let ![]() be the number of real and
be the number of real and ![]() the number of complex conjugate
embeddings of
the number of complex conjugate
embeddings of ![]() into
into
![]() , so
, so
![]() .
Define a map
.
Define a map
To prove Theorem 12.1.2, it suffices to proove that
Im![]() is a lattice in the hyperplane
is a lattice in the hyperplane ![]() from
(12.1.1), which we view as a vector space of dimension
from
(12.1.1), which we view as a vector space of dimension
![]() .
.
Define an embedding
| Re |
To finish the proof of Theorem 12.1.2, we will show that the
image of ![]() spans
spans ![]() . Let
. Let ![]() be the
be the
![]() -span of the image
-span of the image
![]() , and note that
, and note that ![]() is a subspace of
is a subspace of ![]() . We will show
that
. We will show
that ![]() indirectly by showing that if
indirectly by showing that if
![]() ,
where
,
where ![]() is with respect to the dot product on
is with respect to the dot product on
![]() , then
, then
![]() . This will show that
. This will show that
![]() , hence that
, hence that
![]() , as required.
, as required.
Thus suppose
![]() .
Define a function
.
Define a function
![]() by
by
Let
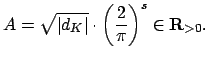
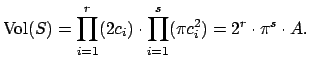
Recall that if ![]() is a lattice and
is a lattice and ![]() is closed,
bounded, etc., and has volume at least
is closed,
bounded, etc., and has volume at least
![]() , then
, then
![]() contains a nonzero element. To apply this lemma, we
take
contains a nonzero element. To apply this lemma, we
take
![]() , where
, where ![]() is as in (12.1.2).
We showed, when proving finiteness of the class group, that
is as in (12.1.2).
We showed, when proving finiteness of the class group, that
![]() . To check the hypothesis
to Blichfeld's lemma, note that
. To check the hypothesis
to Blichfeld's lemma, note that
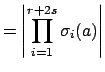 |
||
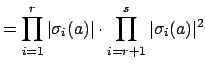 |
||
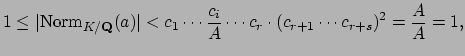
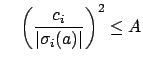 for
for
Our strategy is to use an appropriately chosen ![]() to construct a unit
to construct a unit
![]() such
such
![]() . First, let
. First, let
![]() be
representative generators for the finitely many nonzero principal
ideals of
be
representative generators for the finitely many nonzero principal
ideals of ![]() of norm at most
of norm at most ![]() . Since
. Since
![]() ,
we have
,
we have ![]() , for some
, for some ![]() , so there is a unit
, so there is a unit
![]() such
that
such
that ![]() .
.
Let
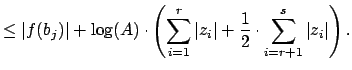 |
The amazing thing about (12.1.4) is that the bound ![]() on the right
hand side does not depend on the
on the right
hand side does not depend on the ![]() .
Suppose we can choose positive real numbers
.
Suppose we can choose positive real numbers ![]() such that
such that
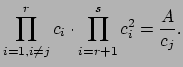
William Stein 2004-05-06