Bibliography

1

A. Agashe and W.A. Stein, Visibility of Shafarevich-Tate groups of abelian varieties: Evidence for the Birch and Swinnerton-Dyer conjecture, (2001).

2

S. Bosch, W. Lütkebohmert, and M. Raynaud, Néron models, Springer-Verlag, Berlin, 1990.

3

C. Chevalley, Une démonstration d'un théorème sur les groupes algébriques, J. Math. Pures Appl. (9) 39 (1960), 307-317.

4

B. Conrad, A modern proof of Chevalley's theorem on algebraic groups,
http://www-math.mit.edu/~dejong/papers/chev.dvi

5

B. Edixhoven, L'action de l'algèbre de Hecke sur les groupes de composantes des jacobiennes des courbes modulaires est ``Eisenstein'', Astérisque (1991), no. 196-197, 7-8, 159-170 (1992), Courbes modulaires et courbes de Shimura (Orsay, 1987/1988).

6

M. Emerton, Optimal quotients of modular Jacobians, (2001), preprint.

7

E.V. Flynn, F. Leprévost, E.F. Schaefer, W.A. Stein, M. Stoll, and J.L. Wetherell, Empirical evidence for the Birch and Swinnerton-Dyer conjectures for modular Jacobians of genus 2 curves, Math. Comp. 70 (2001), no. 236, 1675-1697 (electronic).

8

A. Grothendieck, Éléments de géométrie algébrique, Publications Mathématiques IHES, 4,8,11,17,20,24,28,32, 1960-7.

9

A. Grothendieck, Groupes de monodromie en géométrie algébrique, Lecture Notes in Math 288, Springer-Verlag, Heidelberg (1972).

10

N. Katz, B. Mazur, Arithmetic moduli of elliptic curves, Princetion University Press, Princeton, New Jersey, 1985.

11

D.R. Kohel, Hecke module structure of quaternions, In K. Miyake, ed., Class Field Theory - Its Centenary and Prospect, The Advanced Studies in Pure Mathematics Series, Math Soc. Japan.

12

D.R. Kohel and W.A. Stein, Component Groups of Quotients of $J_0(N)$, Proceedings of the 4th International Symposium (ANTS-IV), Leiden, Netherlands, July 2-7, 2000 (Berlin), Springer, 2000.

13

B. Mazur, Modular curves and the Eisenstein ideal, Inst. Hautes Études Sci. Publ. Math. (1977), no. 47, 33-186 (1978).

14

J.-F. Mestre, La méthode des graphes. Exemples et applications, Proceedings of the international conference on class numbers and fundamental units of algebraic number fields (Katata) (1986), 217-242.

15

J.-F. Mestre and J. Oesterlé, Courbes de Weil semi-stables de discriminant une puissance 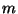$m$-ième, J. Reine Angew. Math. 400 (1989), 173-184.

16

D. Mumford, Abelian varieties, Published for the Tata Institute of Fundamental Research, Bombay, 1970, Tata Institute of Fundamental Research Studies in Mathematics, No. 5.

17

K.A. Ribet, Letter about component groups of elliptic curves,
arXiv:math.AG/0105124v1 (2001).

18

J. Tate, Algorithm for determining the type of a singular fiber in an elliptic pencil, Modular functions of one variable, IV (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Springer, Berlin, 1975, pp. 33-52. Lecture Notes in Math., Vol. 476.