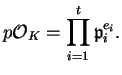![$\displaystyle \xymatrix{
{(??)\, }\ar@{^(->}[r]\ar[d] &{\Spec(\O_K)}\ar[d] \\
...
...]/g(x))\\
{\Spec(\mathbb{Z}/p\mathbb{Z})\,}\ar@{^(->}[r]&{\Spec(\mathbb{Z})}
}$](img38.png)
![$\displaystyle \xymatrix{
{(??)\, }\ar@{^(->}[r]\ar[d] &{\Spec(\O_K)}\ar[d] \\
...
...]/g(x))\\
{\Spec(\mathbb{Z}/p\mathbb{Z})\,}\ar@{^(->}[r]&{\Spec(\mathbb{Z})}
}$](img38.png)
The cover
![]() is easy to understand
because it is defined by the single
equation
is easy to understand
because it is defined by the single
equation ![]() . To give a maximal ideal
. To give a maximal ideal
![]() of
of
![]() such that
such that
![]() is the same as giving a homomorphism
is the same as giving a homomorphism
![]() , which is in turn the same as giving
a root of
, which is in turn the same as giving
a root of ![]() in
in
![]() (an allowed place where
(an allowed place where ![]() can go).
If the index of
can go).
If the index of
![]() in
in ![]() is coprime to
is coprime to ![]() ,
then the primes
,
then the primes
![]() in the factorization of
in the factorization of ![]() don't decompose further going from
don't decompose further going from
![]() to
to ![]() ,
so we are done (the homomorphisms
,
so we are done (the homomorphisms
![]() are
in bijection with the homomorphisms
are
in bijection with the homomorphisms
![]() ).
We formalize this in the following theorem:
).
We formalize this in the following theorem:
![$\displaystyle \overline{g} = \prod_{i=1}^t \overline{g}_i^{e_i} \in (\mathbb{Z}/p\mathbb{Z})[x]
$](img53.png)