Essential Discriminant Divisors

Definition 4.1   A prime $p$ is an essential discriminant divisor if $p\mid [\O _K : \mathbb{Z}[\alpha]]$ for every $\alpha\in\O _K$.

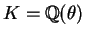
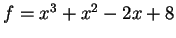
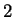
Example 4.2 (Dedekind)   Let $K=\mathbb{Q}(\theta)$ be the cubic field defined by the polynomial $f = x^3 + x^2 - 2x+8$. We will use MAGMA, which implements the algorithm described in the previous section, to show that $2$ is an essential discriminant divisor for $K$.

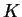
> K := NumberField(x^3 + x^2 - 2*x + 8);
> OK := MaximalOrder(K);
> Factorization(2*OK);
[
<Prime Ideal of OK
Basis:
[2 0 0]
[0 1 0]
[0 0 1], 1>,
<Prime Ideal of OK
Basis:
[1 0 1]
[0 1 0]
[0 0 2], 1>,
<Prime Ideal of OK
Basis:
[1 0 1]
[0 1 1]
[0 0 2], 1>
]

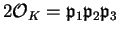
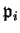
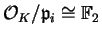
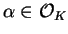
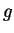
Thus $2\O _K=\mathfrak{p}_1\mathfrak{p}_2\mathfrak{p}_3$ with the $\mathfrak{p}_i$ distinct and $\O _K/\mathfrak{p}_i\cong \mathbb{F}_2$. If $\O _K=\mathbb{Z}[\alpha]$ for some $\alpha\in\O _K$ with minimal polynomial $g$, then $\overline{g}(x)\in\mathbb{F}_2[x]$ must be a product of three distinct linear factors, which is impossible.