| [3] | The Birch and Swinnerton-Dyer Conjecture for 37A
This worksheet illustrates the conjecture of Birch and Swinnerton-Dyer
for the elliptic curve
The Birch and Swinnerton-Dyer Conjecture for 37A
This worksheet illustrates the conjecture of Birch and Swinnerton-Dyer
for the elliptic curve
|
| [24] |
An elliptic curve
with EXAMPLE: with EXAMPLE: |
E = EllipticCurve([0,0,1,-1,0]) G = plot(E, rgbcolor=(1,0,1), thickness=3) show(G,dpi=160)
| [0] | 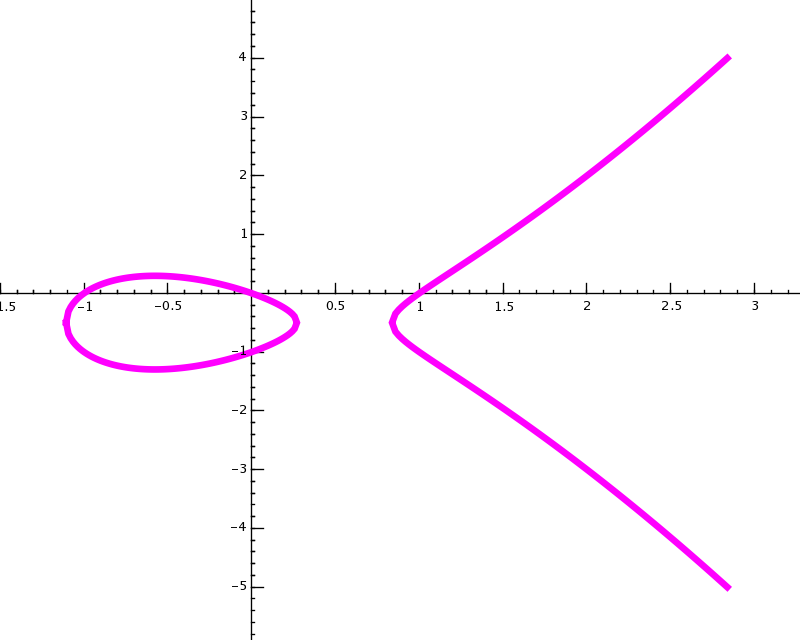
|
E = EllipticCurve([0,0,1,-1,0])
P = E([0,0])
Q = P
for n in range(30):
print '%-10s%-60s'%(n, Q)
Q += P| [8] | 0 (0 : 0 : 1) 1 (1 : 0 : 1) 2 (-1 : -1 : 1) 3 (2 : -3 : 1) 4 (1/4 : -5/8 : 1) 5 (6 : 14 : 1) 6 (-5/9 : 8/27 : 1) 7 (21/25 : -69/125 : 1) 8 (-20/49 : -435/343 : 1) 9 (161/16 : -2065/64 : 1) 10 (116/529 : -3612/12167 : 1) 11 (1357/841 : 28888/24389 : 1) 12 (-3741/3481 : -43355/205379 : 1) 13 (18526/16641 : -2616119/2146689 : 1) 14 (8385/98596 : -28076979/30959144 : 1) 15 (480106/4225 : 332513754/274625 : 1) 16 (-239785/2337841 : 331948240/3574558889 : 1) 17 (12551561/13608721 : -8280062505/50202571769 : 1) 18 (-59997896/67387681 : -641260644409/553185473329 : 1) 19 (683916417/264517696 : -18784454671297/4302115807744 : 1) 20 (1849037896/6941055969 : -318128427505160/578280195945297 : 1) 21 (51678803961/12925188721 : 10663732503571536/1469451780501769 : 1) 22 (-270896443865/384768368209 : 66316334575107447/238670664494938073 : 1) 23 (4881674119706/5677664356225 : -8938035295591025771/13528653463047586625 : 1) 24 (-16683000076735/61935294530404 : -588310630753491921045/487424450554237378792 : 1) 25 (997454379905326/49020596163841 : -31636113722016288336230/343216282443844010111 : 1) 26 (2786836257692691/16063784753682169 : -435912379274109872312968/2035972062206737347698803 : 1) 27 (213822353304561757/158432514799144041 : 41974401721854929811774227/63061816101171948456692661 : 1) 28 (-3148929681285740316/2846153597907293521 : -2181616293371330311419201915/4801616835579099275862827431 : 1) 29 (79799551268268089761/62586636021357187216 : -754388827236735824355996347601/495133617181351428873673516736 : 1) 0 (0 : 0 : 1) 1 (1 : 0 : 1) 2 (-1 : -1 : 1) 3 (2 : -3 : 1) 4 (1/4 : -5/8 : 1) 5 (6 : 14 : 1) 6 (-5/9 : 8/27 : 1) 7 (21/25 : -69/125 : 1) 8 (-20/49 : -435/343 : 1) 9 (161/16 : -2065/64 : 1) 10 (116/529 : -3612/12167 : 1) 11 (1357/841 : 28888/24389 : 1) 12 (-3741/3481 : -43355/205379 : 1) 13 (18526/16641 : -2616119/2146689 : 1) 14 (8385/98596 : -28076979/30959144 : 1) 15 (480106/4225 : 332513754/274625 : 1) 16 (-239785/2337841 : 331948240/3574558889 : 1) 17 (12551561/13608721 : -8280062505/50202571769 : 1) 18 (-59997896/67387681 : -641260644409/553185473329 : 1) 19 (683916417/264517696 : -18784454671297/4302115807744 : 1) 20 (1849037896/6941055969 : -318128427505160/578280195945297 : 1) 21 (51678803961/12925188721 : 10663732503571536/1469451780501769 : 1) 22 (-270896443865/384768368209 : 66316334575107447/238670664494938073 : 1) 23 (4881674119706/5677664356225 : -8938035295591025771/13528653463047586625 : 1) 24 (-16683000076735/61935294530404 : -588310630753491921045/487424450554237378792 : 1) 25 (997454379905326/49020596163841 : -31636113722016288336230/343216282443844010111 : 1) 26 (2786836257692691/16063784753682169 : -435912379274109872312968/2035972062206737347698803 : 1) 27 (213822353304561757/158432514799144041 : 41974401721854929811774227/63061816101171948456692661 : 1) 28 (-3148929681285740316/2846153597907293521 : -2181616293371330311419201915/4801616835579099275862827431 : 1) 29 (79799551268268089761/62586636021357187216 : -754388827236735824355996347601/495133617181351428873673516736 : 1) |
E = EllipticCurve([0,0,1,-1,0])
G = plot(E, thickness=.6, rgbcolor=(1,0,1))
Q = P
n = 100
for i in range(n):
Q = Q + P
if abs(Q[0]) < 3 and abs(Q[1]) < 5:
G += point(Q,rgbcolor=(1,0,0),pointsize=10+float(i)*100/n)
show(G,dpi=150)| [11] | 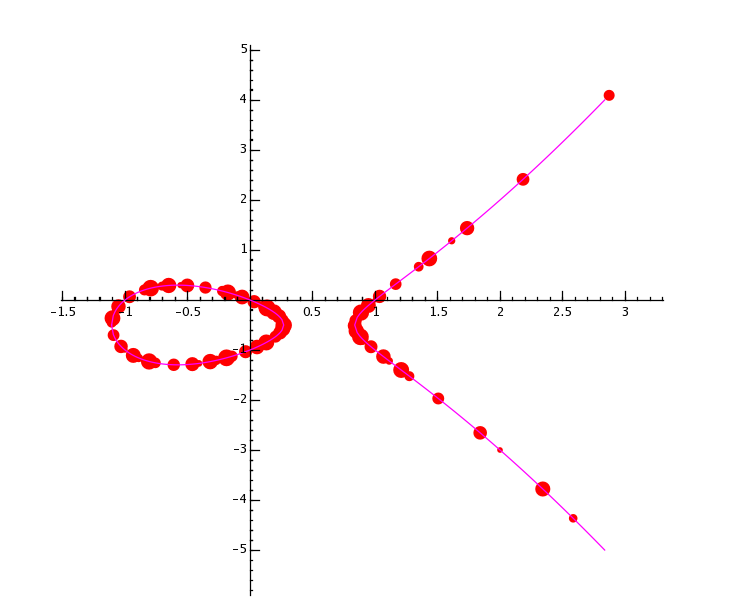
|
t = Tachyon(xres=1000, yres=800, camera_center=(2,7,4), look_at=(2,0,0), raydepth=4)
t.light((10,3,2), 1, (1,1,1))
t.light((10,-3,2), 1, (1,1,1))
t.texture('black', color=(0,0,0))
t.texture('red', color=(1,0,0))
t.texture('grey', color=(.9,.9,.9))
t.plane((0,0,0),(0,0,1),'grey')
t.cylinder((0,0,0),(1,0,0),.01,'black')
t.cylinder((0,0,0),(0,1,0),.01,'black')
E = EllipticCurve('37a')
P = E([0,0])
Q = P
n = 100
for i in range(n):
Q = Q + P
c = i/n + .1
t.texture('r%s'%i,color=(float(i/n),0,0))
t.sphere((Q[0], -Q[1], .01), .04, 'r%s'%i)
t.save()| [6] | 
|
| [7] | A Sharp Contrast:
Question 1: Is there an a priori way to tell which type
of elliptic curve we are dealing with?
|
| [13] |
The L-function
of an elliptic curve is a
function on the complex numbers
defined by counting points modulo primes:
Formally: Formally: |
# Some Pictures of Counting Points
E = EllipticCurve([0,0,1,-1,0])
G = [plot(E.change_ring(GF(p)), pointsize=30, rgbcolor=(1,0,0))\
for p in primes(42) if p!=37]
show(graphics_array(G,4,3),fontsize=4)| [14] | 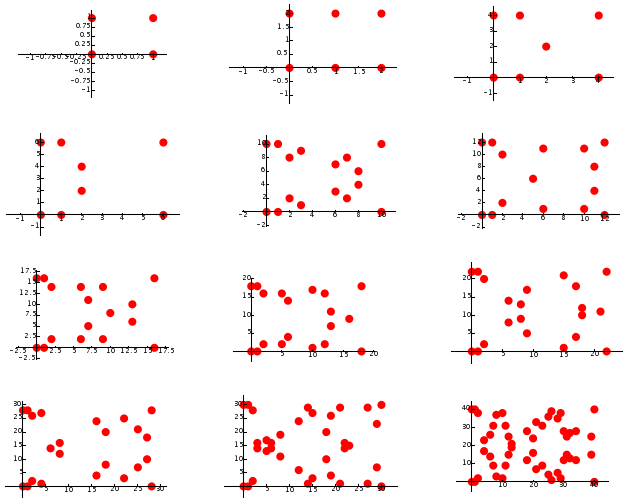
|
# Tally up the number of points (including point at infinity)
E = EllipticCurve([0,0,1,-1,0])
print '.'*40
print '%10s%-2s%10s%13s'%('','p','N_p', 'p+1-N_p')
for p in primes(1000):
print '%10s%-10s%-10s%-10s'%('',p,E.Np(p),E.ap(p))| [16] | ........................................
p N_p p+1-N_p
2 5 -2
3 7 -3
5 8 -2
7 9 -1
11 17 -5
13 16 -2
17 18 0
19 20 0
23 22 2
29 24 6
31 36 -4
37 39 -1
41 51 -9
43 42 2
47 57 -9
53 53 1
59 52 8
61 70 -8
67 60 8
71 63 9
73 75 -1
79 76 4
83 99 -15
89 86 4
97 94 4
101 99 3
103 86 18
107 120 -12
109 126 -16
113 132 -18
127 127 1
131 144 -12
137 144 -6
139 136 4
149 155 -5
151 136 16
157 135 23
163 182 -18
167 180 -12
173 165 9
179 162 18
181 177 5
191 196 -4
193 220 -26
197 195 3
199 198 2
211 225 -13
223 241 -17
227 244 -16
229 223 7
233 228 6
239 246 -6
241 228 14
251 254 -2
257 258 0
263 245 19
269 276 -6
271 303 -31
277 266 12
281 270 12
283 280 4
293 296 -2
307 325 -17
311 312 0
313 292 22
317 296 22
331 334 -2
337 363 -25
347 358 -10
349 344 6
353 346 8
359 375 -15
367 360 8
373 393 -19
379 365 15
383 364 20
389 386 4
397 403 -5
401 384 18
409 390 20
419 413 7
421 446 -24
431 462 -30
433 425 9
439 412 28
443 443 1
449 414 36
457 440 18
461 432 30
463 486 -22
467 470 -2
479 466 14
487 512 -24
491 520 -28
499 488 12
503 488 16
509 541 -31
521 555 -33
523 546 -22
541 522 20
547 540 8
557 576 -18
563 594 -30
569 594 -24
571 565 7
577 578 0
587 620 -32
593 599 -5
599 599 1
601 624 -22
607 640 -32
613 599 15
617 601 17
619 621 -1
631 660 -28
641 643 -1
643 630 14
647 656 -8
653 678 -24
659 675 -15
661 690 -28
673 647 27
677 689 -11
683 666 18
691 712 -20
701 714 -12
709 670 40
719 681 39
727 712 16
733 727 7
739 749 -9
743 723 21
751 727 25
757 808 -50
761 797 -35
769 744 26
773 783 -9
787 793 -5
797 746 52
809 808 2
811 765 47
821 869 -47
823 840 -16
827 806 22
829 834 -4
839 796 44
853 828 26
857 906 -48
859 880 -20
863 888 -24
877 828 50
881 896 -14
883 836 48
887 863 25
907 856 52
911 886 26
919 978 -58
929 912 18
937 901 37
941 952 -10
947 936 12
953 893 61
967 982 -14
971 980 -8
977 950 28
983 975 9
991 1010 -18
997 1040 -42
........................................
p N_p p+1-N_p
2 5 -2
3 7 -3
5 8 -2
7 9 -1
11 17 -5
13 16 -2
17 18 0
19 20 0
23 22 2
29 24 6
31 36 -4
37 39 -1
41 51 -9
43 42 2
47 57 -9
53 53 1
59 52 8
61 70 -8
67 60 8
71 63 9
73 75 -1
79 76 4
83 99 -15
89 86 4
97 94 4
101 99 3
103 86 18
107 120 -12
109 126 -16
113 132 -18
127 127 1
131 144 -12
137 144 -6
139 136 4
149 155 -5
151 136 16
157 135 23
163 182 -18
167 180 -12
173 165 9
179 162 18
181 177 5
191 196 -4
193 220 -26
197 195 3
199 198 2
211 225 -13
223 241 -17
227 244 -16
229 223 7
233 228 6
239 246 -6
241 228 14
251 254 -2
257 258 0
263 245 19
269 276 -6
271 303 -31
277 266 12
281 270 12
283 280 4
293 296 -2
307 325 -17
311 312 0
313 292 22
317 296 22
331 334 -2
337 363 -25
347 358 -10
349 344 6
353 346 8
359 375 -15
367 360 8
373 393 -19
379 365 15
383 364 20
389 386 4
397 403 -5
401 384 18
409 390 20
419 413 7
421 446 -24
431 462 -30
433 425 9
439 412 28
443 443 1
449 414 36
457 440 18
461 432 30
463 486 -22
467 470 -2
479 466 14
487 512 -24
491 520 -28
499 488 12
503 488 16
509 541 -31
521 555 -33
523 546 -22
541 522 20
547 540 8
557 576 -18
563 594 -30
569 594 -24
571 565 7
577 578 0
587 620 -32
593 599 -5
599 599 1
601 624 -22
607 640 -32
613 599 15
617 601 17
619 621 -1
631 660 -28
641 643 -1
643 630 14
647 656 -8
653 678 -24
659 675 -15
661 690 -28
673 647 27
677 689 -11
683 666 18
691 712 -20
701 714 -12
709 670 40
719 681 39
727 712 16
733 727 7
739 749 -9
743 723 21
751 727 25
757 808 -50
761 797 -35
769 744 26
773 783 -9
787 793 -5
797 746 52
809 808 2
811 765 47
821 869 -47
823 840 -16
827 806 22
829 834 -4
839 796 44
853 828 26
857 906 -48
859 880 -20
863 888 -24
877 828 50
881 896 -14
883 836 48
887 863 25
907 856 52
911 886 26
919 978 -58
929 912 18
937 901 37
941 952 -10
947 936 12
953 893 61
967 982 -14
971 980 -8
977 950 28
983 975 9
991 1010 -18
997 1040 -42
|
| [23] | ASIDE -- big recent theorem of Taylor, Harris, Clozel, Shepherd-Barron ASIDE -- big recent theorem of Taylor, Harris, Clozel, Shepherd-Barron 
|
| [17] |
Recall that
the where where |
# Compute the L-series of E
E = EllipticCurve([0,0,1,-1,0])
L = E.Lseries_dokchitser(10) # Tim Dokchitser
plot(L, -2,3, rgbcolor=(0,0,1), plot_points=90, \
plot_division=0, thickness=2).show()| [18] | 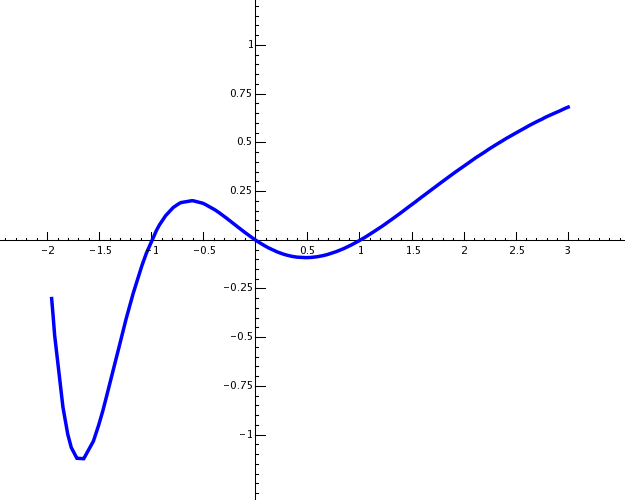
|
t = Tachyon(xres=800, yres=600, camera_center=(1.2,.4,.4), look_at=(1,0,0), raydepth=2)
t.light((10,3,2), 1, (1,1,1))
t.light((10,-3,2), 1, (1,1,1))
t.texture('black', color=(0,0,0))
t.texture('red', color=(1,0,0))
t.texture('white', color=(1,1,1))
t.plane((0,0,-10),(0,0,1),'white')
t.cylinder((0,0,0),(1,0,0),.001,'black')
t.cylinder((0,0,0),(0,1,0),.001,'black')
n=1000
for i in range(n):
x = random()/2+.8; y = random()/2 - .25
try:
z = L(x+I*y)
m = abs(z)
r = arg(z)+pi
except:
continue
t.texture('r%s'%i,color=(r/7,r,0))
t.sphere((x,-y,m), .009, 'r%s'%i)
t.show()| [19] | 
|
t = Tachyon(xres=800, yres=600, camera_center=(1.2,.4,.4), look_at=(1,0,0), raydepth=2)
t.light((10,3,2), 1, (1,1,1))
t.light((10,-3,2), 1, (1,1,1))
t.texture('black', color=(0,0,0))
t.texture('red', color=(1,0,0))
t.texture('white', color=(1,1,1))
t.plane((0,0,-10),(0,0,1),'white')
t.cylinder((0,0,0),(1,0,0),.001,'black')
t.cylinder((0,0,0),(0,1,0),.001,'black')
n=10000
for i in range(n):
x = random()/2+.8; y = random()/2 - .25
try:
z = L(x+I*y)
m = abs(z)
r = arg(z)+pi
except:
continue
t.texture('r%s'%i,color=(r/7,r,0))
t.sphere((x,-y,m), .005, 'r%s'%i)
t.show()| [26] | 
|
print """
<html><font color=black>
<h1>Birch's Parallel Lines?</h1>
</html>
"""
E = [EllipticCurve('11a'), EllipticCurve('37a'),
EllipticCurve('389a'), EllipticCurve('5077a')]
def f(E, B=1000, **args):
v = []; pr = 1
for p in prime_range(2,B):
pr *= float(p/E.Np(p))
if p >= 5:
v.append((p, pr))
return line(v, **args) + point(v,**args)
G = sum([f(E[i],rgbcolor=(i/4.0,0,1-i/4.0)) for i in range(4)])
show(G,ymin=0,ymax=.25,dpi=200)
| [27] |
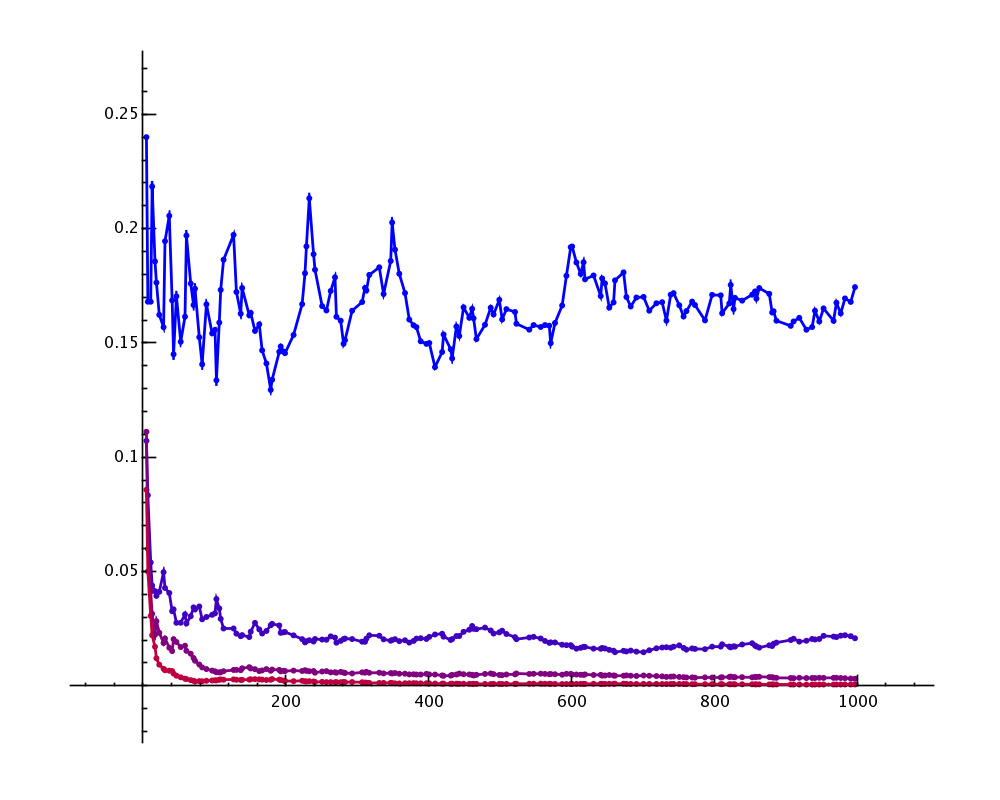
|
| [21] |
Conjecture (Birch and Swinnerton-Dyer):
|
| [22] |