Dirichlet Characters¶
In this chapter we develop a theory for computing with Dirichlet characters, which are extremely important to computations with modular forms for (at least) two reasons:
To compute the Eisenstein subspace
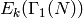 of
of
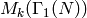 , we write down Eisenstein
series attached to pairs of
Dirichlet characters (the space
, we write down Eisenstein
series attached to pairs of
Dirichlet characters (the space 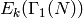 will be
defined in Chapter Eisenstein Series and Bernoulli Numbers).
will be
defined in Chapter Eisenstein Series and Bernoulli Numbers).To compute
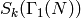 , we instead compute
a decomposition
, we instead compute
a decomposition
and then compute each factor (see Section Dirichlet Character Decomposition). Here the sum is over all Dirichlet characters
 of modulus
of modulus  .
.
Dirichlet characters appear frequently in many other areas of
number theory. For example, by the Kronecker-Weber theorem, Dirichlet
characters correspond to the 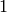 -dimensional representations of
-dimensional representations of
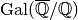 .
.
After defining Dirichlet characters in Section The Definition, in Section Representing Dirichlet Characters we describe a good way to represent Dirichlet characters using a computer. Section Evaluation of Dirichlet Characters is about how to evaluate Dirichlet characters and leads naturally to a discussion of the baby-step giant-step algorithm for solving the discrete log problem and methods for efficiently computing the Kronecker symbol. In Section Conductors of Dirichlet Characters we explain how to factor Dirichlet characters into their prime power constituents and apply this to the computations of conductors. We describe how to carry out a number of standard operations with Dirichlet characters in Section Restriction, Extension, and Galois Orbits and discuss alternative ways to represent them in Section Alternative Representations of Characters. Finally, in Section Dirichlet Characters in Sage we give a very short tutorial about how to compute with Dirichlet characters using Sage.
The Definition¶
Fix an integral domain 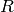 and a root
and a root 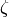 of unity in
of unity in 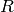 .
.
Definition 4.1
A Dirichlet character of modulus  over
over 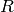 is a map
is a map
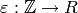 such that there is a homomorphism
such that there is a homomorphism 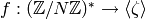 for which
for which
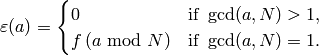
We denote the group of such Dirichlet characters by 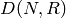 . Note
that elements of
. Note
that elements of 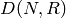 are in bijection with homomorphisms
are in bijection with homomorphisms
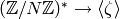 .
.
A familiar Dirichlet character is the Legendre symbol
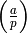 , with
, with  an odd prime, that appears in quadratic
reciprocity theory. It is a Dirichlet character of modulus
an odd prime, that appears in quadratic
reciprocity theory. It is a Dirichlet character of modulus  that
takes the value
that
takes the value 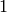 on integers that are congruent to a nonzero square
modulo
on integers that are congruent to a nonzero square
modulo  , the value
, the value 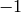 on integers that are congruent to a nonzero
nonsquare modulo
on integers that are congruent to a nonzero
nonsquare modulo  , and
, and 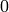 on integers divisible by
on integers divisible by  .
.
Representing Dirichlet Characters¶
Lemma 4.2
The groups 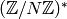 and
and 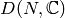 are isomorphic.
are isomorphic.
Proof
We prove the more general fact that for any finite abelian
group 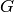 , we have that
, we have that 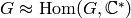 . To deduce this
latter isomorphism, first reduce to the case
when
. To deduce this
latter isomorphism, first reduce to the case
when 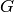 is cyclic by writing
is cyclic by writing 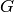 as a product of
cyclic groups. The cyclic case follows
because if
as a product of
cyclic groups. The cyclic case follows
because if 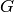 is cyclic of order
is cyclic of order 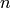 , then
, then
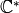 contains an
contains an 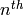 root of unity,
so
root of unity,
so 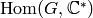 is also cyclic of order
is also cyclic of order 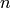 .
Any two cyclic groups of the same order are isomorphic,
so
.
Any two cyclic groups of the same order are isomorphic,
so 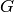 and
and 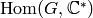 are isomorphic.
are isomorphic.
Corollary 4.3
We have 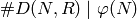 , with equality
if and only if the order of our choice of
, with equality
if and only if the order of our choice of 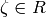 is a multiple of the exponent of the group
is a multiple of the exponent of the group 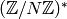 .
.
Proof
This is because 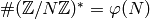 .
.
Fix a positive integer  . To find the set of “canonical”
generators for the group
. To find the set of “canonical”
generators for the group 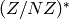 , write
, write 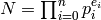 where
where 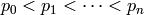 are the prime divisors
of
are the prime divisors
of  . By Exercise 4.2, each factor
. By Exercise 4.2, each factor
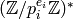 is a cyclic group
is a cyclic group 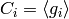 ,
except if
,
except if 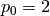 and
and 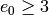 , in which case
, in which case 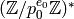 is a product of the cyclic subgroup
is a product of the cyclic subgroup 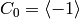 of
order
of
order 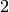 with the cyclic subgroup
with the cyclic subgroup 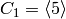 . In all
cases we have
. In all
cases we have
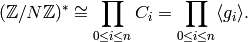
For 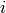 such that
such that 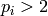 , choose the generator
, choose the generator 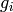 of
of 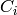 to be
the element of
to be
the element of 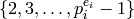 that is smallest and
generates. Finally, use the Chinese Remainder Theorem (see
[Coh93, Section 1.3.3]) to lift each
that is smallest and
generates. Finally, use the Chinese Remainder Theorem (see
[Coh93, Section 1.3.3]) to lift each 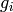 to an element in
to an element in
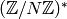 , also denoted
, also denoted 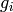 , that is
, that is  modulo each
modulo each 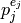 for
for 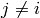 .
.
Algorithm 4.4
Given a prime power 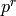 with
with  odd, this algorithm computes
the minimal generator of
odd, this algorithm computes
the minimal generator of 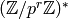 .
.
- [Factor Group Order] Factor
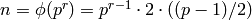 as a product
as a product 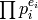 of primes. This is
equivalent in difficulty to factoring
of primes. This is
equivalent in difficulty to factoring 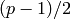 . (See, e.g.,
[Coh93, Ch.8, Ch. 10] for an excellent
discussion of factorization algorithms, though of course much
progress has been made since then.)
. (See, e.g.,
[Coh93, Ch.8, Ch. 10] for an excellent
discussion of factorization algorithms, though of course much
progress has been made since then.) - [Initialize] Set
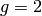 .
. - [Generator?] Using the binary powering algorithm (see
[Coh93, Section 1.2]), compute
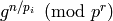 , for each prime divisor
, for each prime divisor 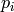 of
of 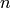 . If
any of these powers are
. If
any of these powers are 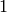 , then
, then 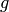 is not a generator, so set
is not a generator, so set
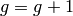 and go to step (2). If no powers
are
and go to step (2). If no powers
are 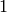 , output
, output 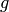 and terminate.
and terminate.
See Exercise 4.3 for a proof that this algorithm is correct.
Example 4.5
A minimal generator for 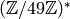 is
is 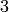 .
We have
.
We have 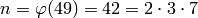 and
and

so 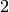 is not a generator for
is not a generator for 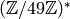 . (We see
this just from
. (We see
this just from 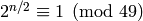 .) However
.) However 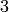 is
a generator since
is
a generator since
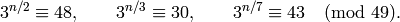
Example 4.6
In this example
we compute minimal generators for  ,
, 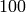 , and
, and 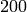 :
:
- The minimal generator for
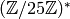 is
is 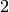 .
. - The minimal generators for
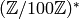 , lifted to numbers
modulo
, lifted to numbers
modulo 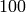 , are
, are 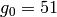 and
and 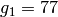 . Notice that
. Notice that
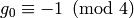 and
and 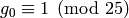 and that
and that
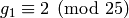 is the minimal generator modulo
is the minimal generator modulo 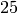 .
. - The minimal generators for
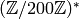 , lifted to numbers
modulo
, lifted to numbers
modulo 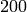 , are
, are 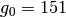 ,
, 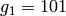 , and
, and 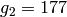 . Note
that
. Note
that 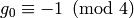 , that
, that 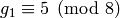 and
and
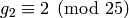 .
.
In Sage, the command Integers(N) creates 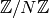 .
.
sage: R = Integers(49)
sage: R
Ring of integers modulo 49
The unit_gens command computes the minimal generators for
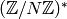 , as defined above.
, as defined above.
sage: R.unit_gens()
[3]
sage: Integers(25).unit_gens()
[2]
sage: Integers(100).unit_gens()
[51, 77]
sage: Integers(200).unit_gens()
[151, 101, 177]
sage: Integers(2005).unit_gens()
[402, 1206]
sage: Integers(200000000).unit_gens()
[174218751, 51562501, 187109377]
Fix an element 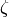 of finite multiplicative order in a ring
of finite multiplicative order in a ring 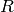 ,
and let
,
and let 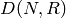 denote the group of Dirichlet characters of modulus
denote the group of Dirichlet characters of modulus  over
over 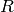 , with image in
, with image in 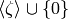 .
In most of this chapter, we
specify an element
.
In most of this chapter, we
specify an element 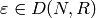 by giving the list
by giving the list
(1)![[\eps(g_0), \eps(g_1), \ldots, \eps(g_n)]](_images/math/bcd42e477f3445ccc81fac340897de59eb314adf.png)
of images of the generators of 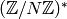 . (Note that if
. (Note that if  is
even, the number of elements of the list (1)
does depend on whether or not
is
even, the number of elements of the list (1)
does depend on whether or not 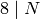 —there are two factors
corresponding to
—there are two factors
corresponding to 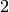 if
if 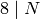 , but only one if
, but only one if 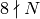 .) This
representation completely determines
.) This
representation completely determines  and is convenient for
arithmetic operations. It is analogous to representing a linear
transformation by a matrix.
and is convenient for
arithmetic operations. It is analogous to representing a linear
transformation by a matrix.
Remark 4.7
In any actual implementation (e.g., the one in Sage), it
is better to represent the 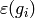 by recording an integer
by recording an integer
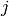 such that
such that 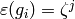 , where
, where 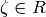 is a fixed root of unity. Then (1) is
internally represented as an element of
is a fixed root of unity. Then (1) is
internally represented as an element of 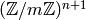 , where
, where
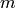 is the multiplicative order of
is the multiplicative order of 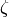 . When
the representation of (1) is needed for an algorithm,
it can be quickly computed on the fly using a table of the powers
of
. When
the representation of (1) is needed for an algorithm,
it can be quickly computed on the fly using a table of the powers
of 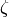 .
See Section Alternative Representations of Characters for further discussion about
ways to represent characters.
.
See Section Alternative Representations of Characters for further discussion about
ways to represent characters.
Example 4.8
The group 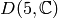 has elements
has elements
![\{[1], [i], [-1], [-i]\}](_images/math/a264a00c7a77b5b757c78c96b9193687455f5106.png) ,
so it is cyclic of order
,
so it is cyclic of order 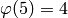 .
In contrast, the group
.
In contrast, the group 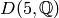 has only the
two elements
has only the
two elements ![[1]](_images/math/97f62c4ffcbe7fb3f0086ce5307e5c37e663debe.png) and
and ![[-1]](_images/math/86d9ee0ec275188d8e1b7d88e89744291542da92.png) and order
and order 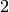 .
.
The command : DirichletGroup(N)
with no second argument creates the group of
Dirichlet characters with values in the
cyclotomic field 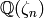 , where
, where 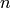 is the exponent of the group
is the exponent of the group 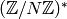 .
Every element in
.
Every element in 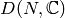 takes values
in
takes values
in 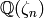 , so
, so 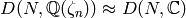 .
.
sage: list(DirichletGroup(5))
[[1], [zeta4], [-1], [-zeta4]]
sage: list(DirichletGroup(5, QQ))
[[1], [-1]]
Evaluation of Dirichlet Characters¶
This section is about how to compute 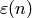 , where
, where  is a Dirichlet character and
is a Dirichlet character and 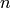 is an integer.
We begin with an example.
is an integer.
We begin with an example.
Example 4.9
If 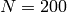 , then
, then 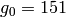 ,
, 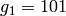 and
and 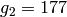 , as
we saw in Example 4.6. The
exponent of
, as
we saw in Example 4.6. The
exponent of 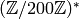 is
is 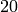 , since that
is the least common multiple of the exponents of
, since that
is the least common multiple of the exponents of
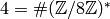 and
and 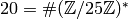 .
The orders of
.
The orders of 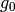 ,
, 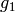 , and
, and 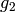 are
are 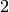 ,
, 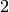 , and
, and 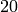 .
Let
.
Let 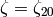 be a primitive
be a primitive 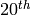 root of
unity in
root of
unity in 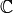 . Then the following are generators
for
. Then the following are generators
for 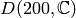 :
:
![\eps_0 = [-1,1,1],\qquad
\eps_1 = [1,-1,1],\qquad
\eps_2 = [1,1,\zeta],](_images/math/af200599401456a4b200330b277965d1d8ef7fcf.png)
and ![\eps=[1,-1,\zeta^5]](_images/math/b759ed73136072fe5c57cfc5dbb251d309d9f862.png) is an example element of order
is an example element of order 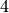 .
To evaluate
.
To evaluate 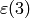 , we write
, we write 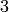 in
terms of
in
terms of 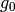 ,
, 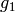 , and
, and 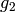 .
First, reducing
.
First, reducing 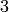 modulo
modulo 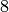 , we see that
, we see that
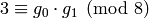 . Next
reducing
. Next
reducing 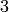 modulo
modulo 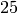 and trying powers of
and trying powers of
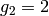 , we find that
, we find that 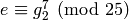 .
Thus
.
Thus
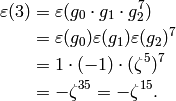
We next illustrate the above computation of 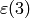 in Sage.
First we make the group
in Sage.
First we make the group 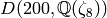 and list its
generators.
and list its
generators.
sage: G = DirichletGroup(200)
sage: G
Group of Dirichlet characters of modulus 200 over
Cyclotomic Field of order 20 and degree 8
sage: G.exponent()
20
sage: G.gens()
([-1, 1, 1], [1, -1, 1], [1, 1, zeta20])
We construct  .
.
sage: K = G.base_ring()
sage: zeta = K.0
sage: eps = G([1,-1,zeta^5])
sage: eps
[1, -1, zeta20^5]
Finally, we evaluate  at
at 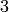 .
.
sage: eps(3)
zeta20^5
sage: -zeta^15
zeta20^5
Example 4.9 illustrates that if  is represented using
a list as described above, evaluation of
is represented using
a list as described above, evaluation of  is inefficient without
extra information; it requires solving the discrete log problem in
is inefficient without
extra information; it requires solving the discrete log problem in
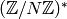 .
.
Remark 4.10
For a general character  , is calculation
of
, is calculation
of  at least as hard as finding discrete
logarithms? Quadratic characters
are easier—see Algorithm 4.23.
at least as hard as finding discrete
logarithms? Quadratic characters
are easier—see Algorithm 4.23.
Algorithm 4.11
Given a Dirichlet character  of modulus
of modulus  , represented
by a list
, represented
by a list ![[\eps(g_0), \eps(g_1), \ldots, \eps(g_n)]](_images/math/753898bca1d16a8de3215e33e798345d9d88fe49.png) ,
and an integer
,
and an integer  , this algorithm computes
, this algorithm computes 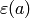 .
.
- [GCD] Compute
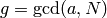 . If
. If 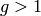 , output
, output 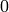 and
terminate.
and
terminate. - [Discrete Log] For each
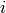 , write
, write 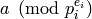 as a
power
as a
power 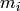 of
of 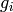 using some algorithm for solving the discrete
log problem (see below). If
using some algorithm for solving the discrete
log problem (see below). If 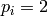 , write
, write
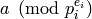 as
as 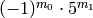 . (This step is
analogous to writing a vector in terms of a basis.)
. (This step is
analogous to writing a vector in terms of a basis.) - [Multiply] Output
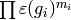 as an element of
as an element of  ,
and terminate. (This is analogous to multiplying a matrix times
a vector.)
,
and terminate. (This is analogous to multiplying a matrix times
a vector.)
The Discrete Log Problem¶
Exercise 4.4 gives an isomorphism of groups
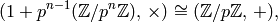
so one sees by induction that step (2) is “about as
difficult” as finding a discrete log in  . There is an
algorithm called “baby-step giant-step”, which solves the discrete
log problem in
. There is an
algorithm called “baby-step giant-step”, which solves the discrete
log problem in 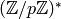 in time
in time 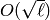 , where
, where 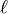 is
the largest prime factor of
is
the largest prime factor of 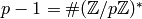 (note that the discrete
log problem in
(note that the discrete
log problem in 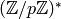 reduces to a series of discrete log
problems in each prime-order cyclic factor). This is unfortunately
still exponential in the number of digits of
reduces to a series of discrete log
problems in each prime-order cyclic factor). This is unfortunately
still exponential in the number of digits of 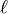 ; it also uses
; it also uses
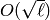 memory. We now describe this algorithm without
any specific optimizations.
memory. We now describe this algorithm without
any specific optimizations.
Algorithm 4.12
Given a prime  , a generator
, a generator 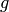 of
of 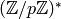 ,
and an element
,
and an element 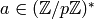 , this algorithm
finds an
, this algorithm
finds an 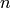 such that
such that 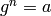 .
(Note that this algorithm works in any cyclic group,
not just
.
(Note that this algorithm works in any cyclic group,
not just 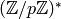 .)
.)
[Make Lists] Let
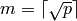 be the ceiling of
be the ceiling of
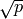 , and construct two lists
, and construct two lists
and
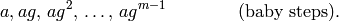
[Find Match] Sort the two lists and find a match
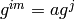 . Then
. Then 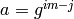 .
.
Proof
We prove that there will always be a match. Since we know that 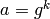 for some
for some 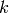 with
with 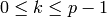 and any such
and any such 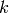 can be written in the form
can be written in the form
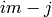 for
for 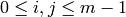 , we will find such a match.
, we will find such a match.
Algorithm 4.12 uses nothing special about
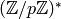 , so it works in a generic group. It is a theorem that
there is no faster algorithm to find discrete logs in a “generic
group” (see [Sho97, Nec94]). There are
much better subexponential algorithms for solving the discrete log
problem in
, so it works in a generic group. It is a theorem that
there is no faster algorithm to find discrete logs in a “generic
group” (see [Sho97, Nec94]). There are
much better subexponential algorithms for solving the discrete log
problem in 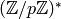 , which use the special structure of this
group. They use the number field sieve (see, e.g.,
[Gor93]), which is also the best-known algorithm for
factoring integers. This class of algorithms has been very well
studied by cryptographers; though sub-exponential, solving discrete
log problems when
, which use the special structure of this
group. They use the number field sieve (see, e.g.,
[Gor93]), which is also the best-known algorithm for
factoring integers. This class of algorithms has been very well
studied by cryptographers; though sub-exponential, solving discrete
log problems when  is large is still extremely difficult. For a
more in-depth survey see [Gor04].
For computing Dirichlet characters in our context,
is large is still extremely difficult. For a
more in-depth survey see [Gor04].
For computing Dirichlet characters in our context,  is not
too large, so Algorithm 4.12 works well.
is not
too large, so Algorithm 4.12 works well.
Enumeration of All Values¶
For many applications of Dirichlet characters to computing modular
forms,  is fairly small, e.g.,
is fairly small, e.g., 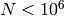 , and we
evaluate
, and we
evaluate  on a huge number of random elements, inside
inner loops of algorithms. Thus for such purposes it will often be
better to make a table of all values of
on a huge number of random elements, inside
inner loops of algorithms. Thus for such purposes it will often be
better to make a table of all values of  , so that evaluation
of
, so that evaluation
of  is extremely fast. The following algorithm computes a table
of all values of
is extremely fast. The following algorithm computes a table
of all values of  , and it does not require computing any
discrete logs since we are computing all values.
, and it does not require computing any
discrete logs since we are computing all values.
Algorithm 4.13
Given a Dirichlet character  represented by the list
of values of
represented by the list
of values of  on the minimal generators
on the minimal generators 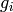 of
of 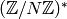 , this algorithm
creates a list of all the values of
, this algorithm
creates a list of all the values of  .
.
[Initialize] For each minimal generator
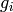 , set
, set 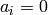 .
Let
.
Let 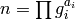 , and set
, and set 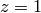 . Create a list
. Create a list  of
of  values, all initially set equal to
values, all initially set equal to 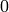 . When this
algorithm terminates, the list
. When this
algorithm terminates, the list  will have the property that
will have the property that![v\,\,[x
\!\!\!\!\!\pmod{N}] = \eps(x).](_images/math/eea4c9d374386c5fc3208d9eafd82c8f5431120c.png)
Notice that we index
 starting at
starting at 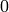 .
.[Add Value to Table] Set
![v[n] \set z](_images/math/13aa4c1947a65225f1e184afb7ec779af6f6492b.png) .
.[Finished?] If each
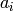 is one less than the order of
is one less than the order of 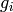 , output
, output  and terminate.
and terminate.[Increment] Set
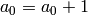 ,
, 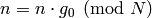 ,
and
,
and 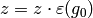 . If
. If 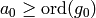 , set
, set
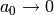 , and then set
, and then set 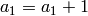 ,
, 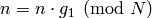 , and
, and 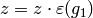 . If
. If 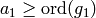 , do what you just did with
, do what you just did with 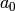 but with all
subscripts replaced by
but with all
subscripts replaced by 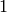 . Etc. (Imagine a car odometer.) Go
to step (2).
. Etc. (Imagine a car odometer.) Go
to step (2).
Conductors of Dirichlet Characters¶
The following algorithm for computing the order of  reduces
the problem to computing the orders of powers of
reduces
the problem to computing the orders of powers of 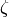 in
in 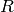 .
.
Algorithm 4.14
This algorithm computes the order of a Dirichlet
character 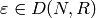 .
.
- Compute the order
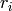 of each
of each 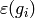 , for each minimal
generator
, for each minimal
generator 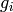 of
of 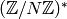 . The order of
. The order of 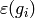 is a
divisor of
is a
divisor of 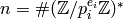 so we can compute its order
by considering the divisors of
so we can compute its order
by considering the divisors of 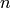 .
. - Compute and output the least common multiple of the integers
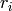 .
.
Remark 4.15
Computing the order of 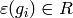 is potentially difficult.
Simultaneously using a different representation of Dirichlet
characters avoids having to compute the order of elements of
is potentially difficult.
Simultaneously using a different representation of Dirichlet
characters avoids having to compute the order of elements of 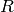 (see Section Alternative Representations of Characters).
(see Section Alternative Representations of Characters).
The next algorithm factors  as a product of “local” characters,
one for each prime divisor of
as a product of “local” characters,
one for each prime divisor of  . It is useful for other algorithms,
e.g., for explicit computations with trace formulas
(see [Hij74]). This factorization is easy to compute
because of how we represent
. It is useful for other algorithms,
e.g., for explicit computations with trace formulas
(see [Hij74]). This factorization is easy to compute
because of how we represent  .
.
Algorithm 4.16
Given a Dirichlet character 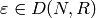 , with
, with 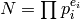 ,
this algorithm finds Dirichlet characters
,
this algorithm finds Dirichlet characters 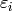 modulo
modulo 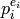 , such
that for all
, such
that for all 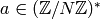 , we have
, we have
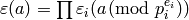 .
If
.
If 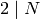 , the steps are as follows:
, the steps are as follows:
Let
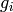 be the minimal generators of
be the minimal generators of 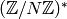 , so
, so  is given by a list
is given by a list![[\eps(g_0),\ldots, \eps(g_n)].](_images/math/8a32946d0b60703c9bb98c944113b4189ff2ecd3.png)
For
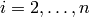 , let
, let 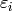 be the element of
be the element of
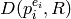 defined by the singleton list
defined by the singleton list ![[\eps(g_i)]](_images/math/bc5a461a23c51bcdf6f7e4e0725c8109bdfcdbda.png) .
.Let
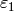 be the element of
be the element of 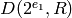 defined by the
list
defined by the
list ![[\eps(g_0), \eps(g_1)]](_images/math/f54b14d6037a16441a7a742302ea3aa7bb57aae0.png) of length
of length 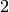 . Output the
. Output the
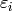 and terminate.
and terminate.
The factorization of Algorithm 4.16 is unique since each
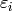 is determined by the image of the canonical map
is determined by the image of the canonical map
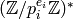 in
in 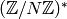 , which sends
, which sends
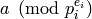 to the element of
to the element of 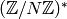 that is
that is
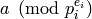 and
and 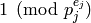 for
for 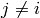 .
.
Example 4.17
If ![\eps = [1,-1,\zeta^5] \in D(200,\C)](_images/math/81562f1437dd368cf3c06c45bda581a07b70f855.png) , then
, then
![\eps_1 = [1,-1]\in D(8,\C)](_images/math/773f6a32510c9523945d21eb4cb154f2c1b22f27.png) and
and ![\eps_2 = [\zeta^5]\in D(25,\C)](_images/math/772ab894e8182d1e3fd16de0454bc716ef701b33.png) .
.
Definition 4.18
The conductor of a Dirichlet character 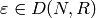 is the smallest positive divisor
is the smallest positive divisor 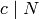 such that
there is a character
such that
there is a character 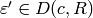 for which
for which
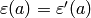 for all
for all 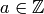 with
with 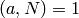 .
A Dirichlet character is primitive if its modulus equals
its conductor. The character
.
A Dirichlet character is primitive if its modulus equals
its conductor. The character 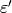 associated to
associated to  with modulus equal to the conductor of
with modulus equal to the conductor of  is called
the primitive character associated to
is called
the primitive character associated to  .
.
We will be interested in conductors later, when computing new
subspaces of spaces of modular forms with character. Also certain
formulas for special values of 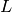 functions are only valid for
primitive characters.
functions are only valid for
primitive characters.
Algorithm 4.19
This algorithm computes the conductor of a Dirichlet
character 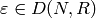 .
.
- [Factor Character] Using Algorithm 4.16, find
characters
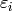 whose product is
whose product is  .
. - [Compute Orders] Using Algorithm 4.14, compute
the orders
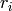 of each
of each 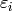 .
. - [Conductors of Factors] For each
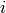 , either set
, either set 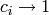 if
if
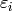 is the trivial character (i.e., of order
is the trivial character (i.e., of order 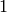 ) or set
) or set
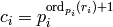 , where
, where 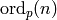 is the
largest power of
is the
largest power of  that divides
that divides 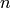 .
. - [Adjust at
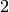 ?] If
?] If 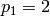 and
and 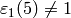 , set
, set
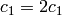 .
. - [Finished] Output
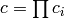 and terminate.
and terminate.
Proof
Let 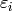 be the local factors of
be the local factors of  , as in step (1)).
We first show that the product of the conductors
, as in step (1)).
We first show that the product of the conductors 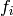 of the
of the 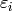 is
the conductor
is
the conductor 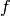 of
of  . Since
. Since 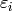 factors through
factors through 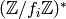 ,
the product
,
the product  of the
of the 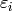 factors through
factors through 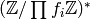 ,
so the conductor of
,
so the conductor of  divides
divides 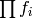 . Conversely, if
. Conversely, if
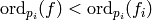 for some
for some 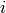 , then we could factor
, then we could factor  as a product of local (prime power) characters differently, which contradicts
that this factorization is unique.
as a product of local (prime power) characters differently, which contradicts
that this factorization is unique.
It remains to prove that if  is a nontrivial character of modulus
is a nontrivial character of modulus
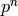 , where
, where  is a prime, and if
is a prime, and if  is the order of
is the order of  , then the
conductor of
, then the
conductor of  is
is 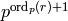 , except possibly if
, except possibly if 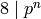 . Since the order and conductor of
. Since the order and conductor of  and of the associated
primitive character
and of the associated
primitive character 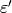 are the same, we may assume
are the same, we may assume  is
primitive, i.e., that
is
primitive, i.e., that 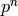 is the conductor of
is the conductor of  ; note that
; note that
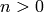 , since
, since  is nontrivial.
is nontrivial.
First suppose  is odd.
Then the abelian group
is odd.
Then the abelian group 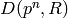 splits as a direct sum
splits as a direct sum 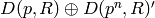 ,
where
,
where 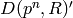 is the
is the  -power torsion subgroup of
-power torsion subgroup of 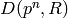 .
Also
.
Also  has order
has order 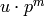 , where
, where 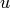 , which
is coprime to
, which
is coprime to  , is the order of the image of
, is the order of the image of  in
in 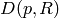 and
and 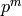 is the order of the image in
is the order of the image in 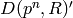 .
If
.
If 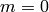 , then the order of
, then the order of  is coprime to
is coprime to  , so
, so
 is in
is in 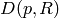 , which means that
, which means that 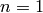 ,
so
,
so 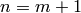 , as required. If
, as required. If 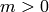 , then
, then 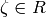 must have order divisible by
must have order divisible by  , so
, so 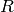 has characteristic not
equal to
has characteristic not
equal to  . The conductor of
. The conductor of  does not change if we
adjoin roots of unity to
does not change if we
adjoin roots of unity to 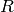 , so in light of Lemma 4.2
we may assume that
, so in light of Lemma 4.2
we may assume that 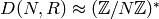 .
It follows that for each
.
It follows that for each 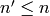 , the
, the  -power subgroup
-power subgroup
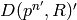 of
of 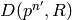 is the
is the 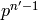 -torsion
subgroup of
-torsion
subgroup of 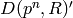 . Thus
. Thus 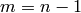 , since
, since
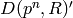 is by assumption the smallest such group that
contains the projection of
is by assumption the smallest such group that
contains the projection of  . This proves the
formula of step ((3). We leave the argument
when
. This proves the
formula of step ((3). We leave the argument
when 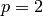 as an exercise (see Exercise 4.5).
as an exercise (see Exercise 4.5).
Example 4.20
If ![\eps = [1,-1,\zeta^5] \in D(200,\C)](_images/math/81562f1437dd368cf3c06c45bda581a07b70f855.png) , then
as in Example 4.17,
, then
as in Example 4.17,  is the product of
is the product of ![\eps_1=[1,-1]](_images/math/8287ff1f3df82492784b4b9b31d79ea576a5b2c1.png) and
and ![\eps_2 = [\zeta^5]](_images/math/400e0885bb15a2a1a934757bd3b9a90614518588.png) .
Because
.
Because 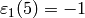 , the conductor of
, the conductor of 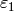 is
is 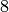 .
The order of
.
The order of 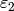 is
is 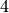 (since
(since 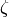 is a
is a 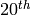 root of unity), so the conductor of
root of unity), so the conductor of 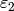 is
is 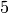 .
Thus the conductor of
.
Thus the conductor of  is
is 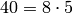 .
.
The Kronecker Symbol¶
In this section all characters have values in 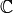 .
.
Frequently quadratic characters are described in terms of the
Kronecker symbol 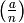 , which we define for any integer
, which we define for any integer  and positive integer
and positive integer 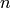 as follows.
First, if
as follows.
First, if 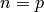 is an odd prime, then for any integer
is an odd prime, then for any integer  ,
,
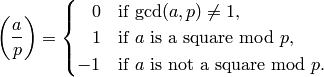
If 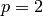 , then
, then
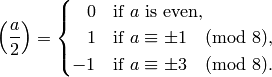
More generally, if 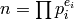 with the
with the 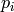 prime,
then
prime,
then
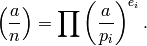
Remark 4.21
One can also extend 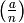 to
to 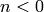 , but we will not need this.
The extension is to set
, but we will not need this.
The extension is to set 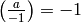 and
and 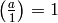 , for
, for
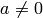 , and to extend multiplicatively (in the denominator).
Note that the map
, and to extend multiplicatively (in the denominator).
Note that the map 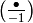 is not a Dirichlet
character (see Exercise 4.1).
is not a Dirichlet
character (see Exercise 4.1).
Let 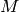 be the product of the primes
be the product of the primes  such
that
such
that 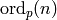 is odd.
If
is odd.
If 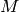 is odd, let
is odd, let 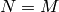 ; otherwise, let
; otherwise, let 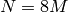 .
.
Lemma 4.22
The function
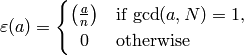
is a Dirichlet character of modulus  .
The function
.
The function
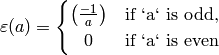
is a Dirichlet character of modulus  .
.
Proof
When restricted to 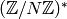 , each map
, each map 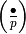 , for
, for
 prime, is a homomorphism, so
prime, is a homomorphism, so  a product of homomorphisms.
The second statement follows from the definition and the
fact that
a product of homomorphisms.
The second statement follows from the definition and the
fact that 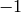 is a
square modulo an odd prime
is a
square modulo an odd prime  if and only if
if and only if 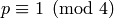 .
.
This section is about going between representing quadratic
characters as row matrices and via Kronecker symbols. This is
valuable because the algorithms in
[Coh93, Section 1.1.4] for computing Kronecker symbols
run in time quadratic in the number of digits of the input.
They do
not require computing discrete logarithms; instead,
they use, e.g., that
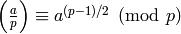 , when
, when  is an odd prime.
is an odd prime.
Algorithm 4.23
Given 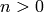 , this algorithm computes a representation of
the Kronecker symbol
, this algorithm computes a representation of
the Kronecker symbol  as a Dirichlet character.
as a Dirichlet character.
- [Modulus] Compute
 as in Lemma 4.22.
as in Lemma 4.22. - [Minimal Generators] Compute minimal generators
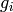 of
of
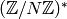 using Algorithm 4.4.
using Algorithm 4.4. - [Images] Compute
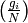 for each
for each 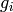 using one
of the algorithms of [Coh93, Section 1.1.4].
using one
of the algorithms of [Coh93, Section 1.1.4].
Example 4.24
We compute the Dirichlet character associated to 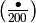 .
Using Sage, we compute the
.
Using Sage, we compute the 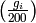 , for
, for 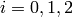 , where the
, where the
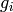 are as in Example 4.9:
are as in Example 4.9:
sage: kronecker(151,200)
1
sage: kronecker(101,200)
-1
sage: kronecker(177,200)
1
Thus the corresponding character is defined by ![[1,-1,1]](_images/math/2586c8e022fc0248c089953537980360a66c2423.png) .
.
Example 4.25
We compute the character associated to 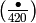 .
We have
.
We have 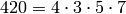 , and minimal generators
are
, and minimal generators
are
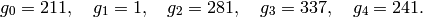
We have 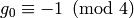 ,
, 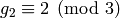 ,
, 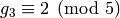 and
and 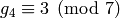 .
We find
.
We find 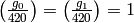 and
and 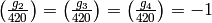 .
The corresponding character is
.
The corresponding character is ![[1,1,-1,-1,-1]](_images/math/99e91b2f0dbbc096a217d759f2184a3269e1d949.png) .
.
Using the following algorithm, we can go in the other direction, i.e., write any quadratic Dirichlet character as a Kronecker symbol.
Algorithm 4.26
Given  of order
of order 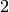 with modulus
with modulus  , this
algorithm writes
, this
algorithm writes  as a Kronecker symbol.
as a Kronecker symbol.
- [Conductor] Use Algorithm 4.19 to compute the conductor
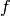 of
of  .
. - [Odd] If
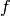 is odd, output
is odd, output 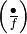 .
. - [Even] If
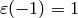 , output
, output 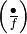 ;
if
;
if 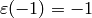 , output
, output
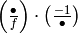 .
.
Proof
Since 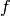 is the conductor of a quadratic Dirichlet character,
it is a square-free product
is the conductor of a quadratic Dirichlet character,
it is a square-free product 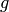 of odd primes times either
of odd primes times either
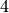 or
or 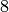 , so the
group
, so the
group 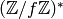 does not inject into
does not inject into 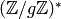 for
any proper divisor
for
any proper divisor 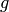 of
of 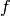 (see this by
reducing to the prime power case).
Since
(see this by
reducing to the prime power case).
Since 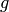 is odd and square-free, the character
is odd and square-free, the character 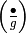 has conductor
has conductor 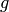 .
For each odd prime
.
For each odd prime  ,
by step (3) of Algorithm 4.19
the factor at
,
by step (3) of Algorithm 4.19
the factor at  of both
of both  and
and 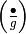 is a quadratic character with modulus
is a quadratic character with modulus  .
By Exercise 4.2 and Lemma 4.2
the group
.
By Exercise 4.2 and Lemma 4.2
the group 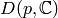 is cyclic, so it has a unique element
of order
is cyclic, so it has a unique element
of order 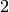 , so
the factors of
, so
the factors of  and
and 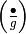 at
at  are equal.
are equal.
The quadratic characters with conductor a power of 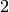 are
are ![[-1]](_images/math/86d9ee0ec275188d8e1b7d88e89744291542da92.png) ,
,
![[1,-1]](_images/math/45a525bcc4bbe740923b17018fdf5461c6acc82c.png) , and
, and ![[-1,-1]](_images/math/f0e55e0774e18250f3aee0d948216987f3322c38.png) . The character
. The character ![[1,-1]](_images/math/45a525bcc4bbe740923b17018fdf5461c6acc82c.png) is
is 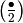 and the character
and the character ![[-1]](_images/math/86d9ee0ec275188d8e1b7d88e89744291542da92.png) is
is 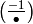 .
.
Example 4.27
Consider ![\eps=[-1,-1,-1,-1,-1]](_images/math/2cab2a523fd25ad807b3abc647ee3eecb292bbf9.png) with modulus
with modulus
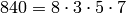 . It has conductor
. It has conductor 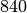 , and
, and
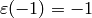 , so for all
, so for all  with
with 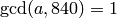 , we have
, we have
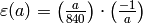 .
.
Restriction, Extension, and Galois Orbits¶
The following two algorithms restrict and extend characters to a
compatible modulus. Using them, it is easy to define multiplication of
two characters 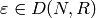 and
and 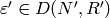 , as long as
, as long as
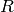 and
and 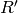 are subrings of a common ring. To carry out the
multiplication, extend both characters to a common base ring,
and then extend them to characters modulo
are subrings of a common ring. To carry out the
multiplication, extend both characters to a common base ring,
and then extend them to characters modulo 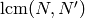 and multiply.
and multiply.
Algorithm 4.28
Given a Dirichlet character 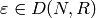 and a divisor
and a divisor
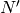 of
of  that is a multiple of the conductor of
that is a multiple of the conductor of  ,
this algorithm finds a characters
,
this algorithm finds a characters 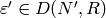 , such
that
, such
that 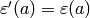 , for all
, for all 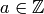 with
with 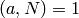 .
.
- [Conductor] Compute the conductor of
 using
Algorithm 4.19, and verify that
using
Algorithm 4.19, and verify that 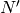 is
divisible by the conductor and divides
is
divisible by the conductor and divides  .
. - [Minimal Generators] Compute minimal generators
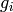 for
for
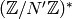 .
. - [Values of Restriction] For each
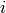 ,
compute
,
compute 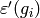 as follows. Find a multiple
as follows. Find a multiple 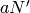 of
of 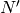 such
that
such
that 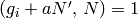 ; then
; then 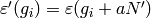 .
. - [Output Character] Output the Dirichlet character of modulus
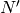 defined by
defined by ![[\eps'(g_0),\ldots, \eps'(g_n)]](_images/math/d72fb0fb48ae9f7754f3dfb17842b9de86bbb0a7.png) .
.
Proof
The only part that is not clear is that in step (3)
there is an  such that
such that 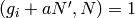 . If
we write
. If
we write 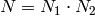 , with
, with 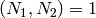 and
and 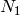 divisible
by all primes that divide
divisible
by all primes that divide 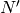 , then
, then 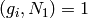 since
since
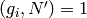 . By the Chinese Remainder Theorem,
there is an
. By the Chinese Remainder Theorem,
there is an 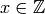 such that
such that 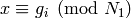 and
and
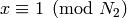 . Then
. Then 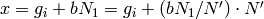 and
and 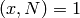 , which completes the proof.
, which completes the proof.
Algorithm 4.29
Given a Dirichlet character 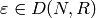 and a multiple
and a multiple
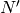 of
of  ,
this algorithm finds a character
,
this algorithm finds a character 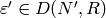 , such
that
, such
that 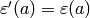 , for all
, for all 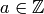 with
with 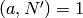 .
.
- Minimal Generators] Compute minimal generators
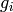 for
for
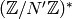 .
. - [Evaluate] Compute
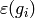 for each
for each 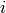 . Since
. Since 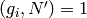 ,
we also have
,
we also have 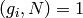 .
. - [Output Character] Output the character
![[\eps(g_0),\ldots, \eps(g_n)]](_images/math/e500b08bfcc4ad4be994d6048d05db8e9b41bb81.png) .
.
Let 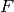 be the prime subfield of
be the prime subfield of 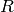 , and assume
that
, and assume
that 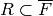 , where
, where 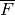 is a separable closure of
is a separable closure of 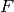 . If
. If 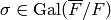 and
and 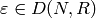 , let
, let 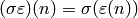 ;
this defines an action of
;
this defines an action of 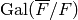 on
on 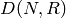 .
Our next algorithm computes the orbits for
the action of
.
Our next algorithm computes the orbits for
the action of 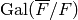 on
on 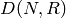 . This
algorithm can provide huge savings for modular
forms computations because the spaces
. This
algorithm can provide huge savings for modular
forms computations because the spaces 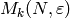 and
and 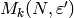 are canonically isomorphic if
are canonically isomorphic if  and
and 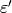 are conjugate.
are conjugate.
Algorithm 4.30
Given a Dirichlet character 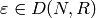 , this algorithm
computes the orbit of
, this algorithm
computes the orbit of  under the action of
under the action of 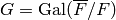 ,
where
,
where 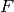 is the prime subfield of
is the prime subfield of 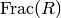 , so
, so 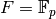 or
or 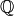 .
.
[Order of
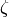 ] Let
] Let 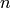 be the order of the chosen root
be the order of the chosen root
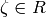 .
.[Nontrivial Automorphisms] If
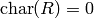 , let
, let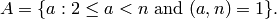
If
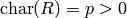 , compute the multiplicative order
, compute the multiplicative order  of
of 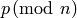 ,
and let
,
and let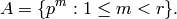
[Compute Orbit] Compute and output the set of unique elements
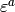 for each
for each 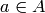 (there could be repeats, so we output
unique elements only).
(there could be repeats, so we output
unique elements only).
Proof
We prove that the nontrivial automorphisms of  in characteristic
in characteristic  are as in step (2). It is
well known that every automorphism in characteristic
are as in step (2). It is
well known that every automorphism in characteristic  on
on
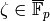 is of the form
is of the form 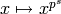 , for some
, for some  .
The images of
.
The images of 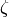 under such automorphisms are
under such automorphisms are
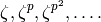
Suppose 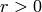 is minimal such that
is minimal such that 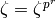 . Then the
orbit of
. Then the
orbit of 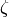 is
is 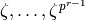 .
Also
.
Also 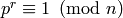 , where
, where 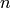 is the multiplicative order of
is the multiplicative order of 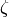 ,
so
,
so  is the multiplicative order of
is the multiplicative order of  modulo
modulo 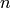 , which completes
the proof.
, which completes
the proof.
Example 4.31
The Galois orbits of characters in 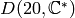 are as follows:
are as follows:
![G_0 &= \{ [1,1,1]\},\\
G_1 &= \{[-1,1,1]\}, \\
G_2 &= \{[1,1,\zeta_4],\,\, [1,1,-\zeta_4]\}\\
G_3 &= \{[-1,1,\zeta_4],\,\, [-1,1,-\zeta_4]\}\\
G_4 &= \{[1,1,-1]\}, \\
G_5 &= \{[-1,1,-1]\}.](_images/math/dcd53600e93729e60eab3350dd29e19e1225427d.png)
The conductors of the characters in orbit 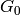 are
are 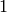 , in
orbit
, in
orbit 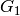 they are
they are 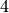 , in orbit
, in orbit 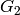 they are
they are 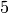 , in
, in
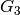 they are
they are 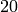 , in
, in 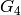 the conductor is
the conductor is 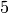 ,
and in
,
and in 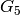 the conductor is
the conductor is 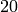 . (You should verify this.)
. (You should verify this.)
Sage computes Galois orbits as follows:
sage: G = DirichletGroup(20)
sage: G.galois_orbits()
[
[[1, 1]],
[[1, zeta4], [1, -zeta4]],
[[1, -1]],
[[-1, 1]],
[[-1, zeta4], [-1, -zeta4]],
[[-1, -1]]
]
Alternative Representations of Characters¶
Let  be a positive integer and
be a positive integer and 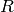 an integral domain, with fixed
root of unity
an integral domain, with fixed
root of unity 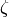 of
order
of
order 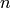 , and let
, and let 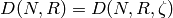 . As in
the rest of this chapter, write
. As in
the rest of this chapter, write 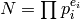 , and let
, and let
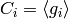 be the corresponding cyclic factors of
be the corresponding cyclic factors of
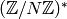 . In this section we discuss other ways to represent
elements
. In this section we discuss other ways to represent
elements 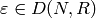 . Each representation has advantages and
disadvantages, and no single representation is best.
It is easy to convert between them, and some algorithms are much
easier using one representation than when using another.
In this section we present two other representations, each
having advantages and disadvantages. There
is no reason to restrict to only one representation; for example,
Sage internally uses both.
. Each representation has advantages and
disadvantages, and no single representation is best.
It is easy to convert between them, and some algorithms are much
easier using one representation than when using another.
In this section we present two other representations, each
having advantages and disadvantages. There
is no reason to restrict to only one representation; for example,
Sage internally uses both.
We could represent  by giving a list
by giving a list ![[b_0,\ldots, b_r]](_images/math/53dfa6e3735369b546035182f4cf5b287ba93d98.png) , where
each
, where
each 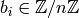 and
and 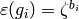 . Then arithmetic in
. Then arithmetic in
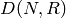 is arithmetic in
is arithmetic in 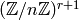 , which is very efficient.
A drawback to this approach (in practice) is that it is easy to
accidently consider sequences that do not actually correspond to
elements of
, which is very efficient.
A drawback to this approach (in practice) is that it is easy to
accidently consider sequences that do not actually correspond to
elements of 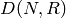 . Also the choice of
. Also the choice of 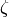 is less clear, which
can cause confusion. Finally, the orders of the local factors is more
opaque, e.g., compare
is less clear, which
can cause confusion. Finally, the orders of the local factors is more
opaque, e.g., compare ![[-1,\zeta_{40}]](_images/math/ad1b100455f028c834c189db257fcdbae5f6dedf.png) with
with ![[20,1]](_images/math/2eaf86a212c40a073f0aa23fdf355bab1dc242bb.png) . Overall this
representation is not too bad and is more like representing a linear
transformation by a matrix. It has the advantage over the
representation discussed earlier in this chapter that arithmetic in
. Overall this
representation is not too bad and is more like representing a linear
transformation by a matrix. It has the advantage over the
representation discussed earlier in this chapter that arithmetic in
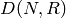 is very efficient and does not require any operations in the
ring
is very efficient and does not require any operations in the
ring 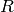 .
.
Another way to represent  would be to give a list
would be to give a list ![[b_0,\ldots,
b_r]](_images/math/54e0603d9b9bf448f5a189daa00cda3b2292af44.png) of integers, but this time with
of integers, but this time with 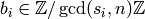 , where
, where
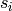 is the order of
is the order of 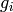 . Then
. Then
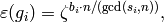
which is already pretty complicated. With this representation we set up an identification
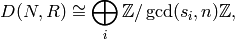
and arithmetic is
efficient. This approach is seductive because every sequence of
integers determines a character, and the sizes of the integers in the
sequence nicely indicate the local orders of the character. However,
giving analogues of many of the algorithms discussed in this chapter
that operate on characters represented this way is tricky. For
example, the representation depends very much on the order of  ,
so it is difficult to correctly compute natural maps
,
so it is difficult to correctly compute natural maps  , for
, for 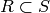 rings.
rings.
Dirichlet Characters in Sage¶
To create a Dirichlet character in Sage, first create
the group 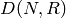 of Dirichlet characters then construct
elements of that group. First we make
of Dirichlet characters then construct
elements of that group. First we make 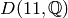 :
:
sage: G = DirichletGroup(11, QQ); G
Group of Dirichlet characters of modulus 11 over
Rational Field
A Dirichlet character prints as a matrix that gives
the values of the character on canonical generators
of 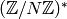 (as discussed below).
(as discussed below).
sage: list(G)
[[1], [-1]]
sage: eps = G.0 # 0th generator for Dirichlet group
sage: eps
[-1]
The character  takes the value
takes the value 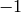 on the
unit generator.
on the
unit generator.
sage: G.unit_gens()
[2]
sage: eps(2)
-1
sage: eps(3)
1
It is 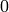 on any integer not coprime to
on any integer not coprime to 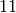 :
:
sage: [eps(11*n) for n in range(10)]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
We can also create groups of Dirichlet characters
taking values in other rings or fields.
For example, we create the cyclotomic field 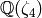 .
.
sage: R = CyclotomicField(4)
sage: CyclotomicField(4)
Cyclotomic Field of order 4 and degree 2
Then we define 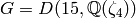 .
.
sage: G = DirichletGroup(15, R)
sage: G
Group of Dirichlet characters of modulus 15 over
Cyclotomic Field of order 4 and degree 2
Next we list each of its elements.
sage: list(G)
[[1, 1], [-1, 1], [1, zeta4], [-1, zeta4], [1, -1],
[-1, -1], [1, -zeta4], [-1, -zeta4]]
Now we evaluate the second generator of 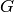 on various
integers:
on various
integers:
sage: e = G.1
sage: e(4)
-1
sage: e(-1)
-1
sage: e(5)
0
Finally we list all the values of  .
.
sage: [e(n) for n in range(15)]
[0, 1, zeta4, 0, -1, 0, 0, zeta4, -zeta4,
0, 0, 1, 0, -zeta4, -1]
We can also compute with groups of Dirichlet characters with values in a finite field.
sage: G = DirichletGroup(15, GF(5)); G
Group of Dirichlet characters of modulus 15
over Finite Field of size 5
We list all the elements of 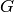 , again represented by lists
that give the images of each unit generator, as an element of
, again represented by lists
that give the images of each unit generator, as an element of 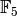 .
.
sage: list(G)
[[1, 1], [4, 1], [1, 2], [4, 2], [1, 4], [4, 4],
[1, 3], [4, 3]]
We evaluate the second generator of 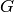 on several integers.
on several integers.
sage: e = G.1
sage: e(-1)
4
sage: e(2)
2
sage: e(5)
0
sage: print [e(n) for n in range(15)]
[0, 1, 2, 0, 4, 0, 0, 2, 3, 0, 0, 1, 0, 3, 4]
Exercises¶
Exercise 4.1
Let 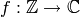 be the map given by
be the map given by
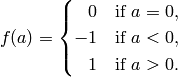
Prove that 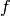 is not a Dirichlet character
of any modulus
is not a Dirichlet character
of any modulus  .
.
Exercise 4.2
This exercise is about the structure of the units of 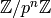 .
.
- If
 is odd and
is odd and 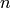 is a positive integer,
prove that
is a positive integer,
prove that 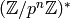 is cyclic.
is cyclic. - For
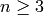 , prove that
, prove that 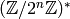 is a direct sum of the
cyclic subgroups
is a direct sum of the
cyclic subgroups 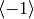 and
and 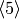 ,
of orders 2 and
,
of orders 2 and 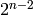 , respectively.
, respectively.
Exercise 4.3
Prove that Algorithm 4.4 works, i.e., that if
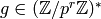 and
and 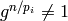 for all
for all
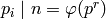 , then
, then 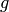 is a generator of
is a generator of 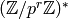 .
.
Exercise 4.4
Let
 be an odd prime and
be an odd prime and 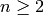 an integer, and prove
that
an integer, and prove
that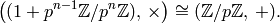
Use the first part to show that solving the discrete log problem in
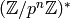 is “not much harder” than solving the
discrete log problem in
is “not much harder” than solving the
discrete log problem in 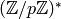 .
.
Exercise 4.5
Suppose  is a nontrivial Dirichlet character of modulus
is a nontrivial Dirichlet character of modulus 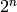 of order
of order  over the complex numbers
over the complex numbers 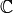 .
Prove that the conductor of
.
Prove that the conductor of  is
is
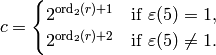
Exercise 4.6
- Find an irreducible quadratic polynomial
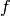 over
over 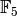 .
. - Then
![\F_{25} = \F_5[x]/(f)](_images/math/b447d3de32e2a09ed98faf1501b63e39ffba334d.png) . Find an element with multiplicative
order
. Find an element with multiplicative
order 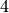 in
in 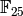 .
. - Make a list of all Dirichlet characters in
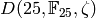 .
. - Divide these characters into orbits for the action of
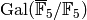 .
.
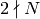 , then omit step
, then omit step