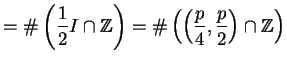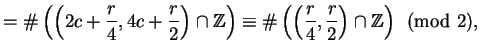Next: The Quadratic Reciprocity Law
Up: Lecture 13: Quadratic Reciprocity
Previous: Recall Gauss's Lemma
Proof.
If
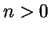
, then
where the union is disjoint. Let
![$ [x]$](img15.png)
denote the least integer
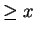
. There are
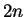
integers,
in the interval
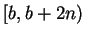
, so
the assertion of the lemma is true in this case.
We also have
and
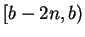
also contains exactly
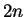
integers,
so the lemma is also true when
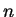
is negative.
The statement about
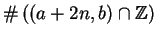
is proved in a similar manner.

The following proposition was first conjectured by Euler, based
on extensive numerical evidence. Once we've proved this proposition,
it will be easy to deduce the quadratic reciprocity law.
Proof.
To apply Gauss's lemma, we have to compute the parity of the intersection
of
and
where
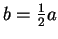
or
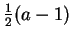
, whichever is an integer.
(Why? We have to check that every element of 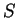 that reduces
to something in the interval
that reduces
to something in the interval
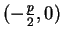 lies in
lies in 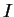 .
This is clear if
.
This is clear if
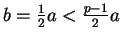 . If
. If
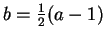 , then
, then
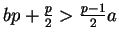 ,
so
,
so
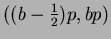 is the last interval that could contain
an element of of
is the last interval that could contain
an element of of  that reduces to
that reduces to
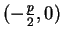 .)
Also note that the integer endpoints of
.)
Also note that the integer endpoints of 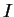 are not in
are not in 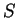 , since
those endpoints are divisible by
, since
those endpoints are divisible by 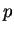 , but no element of
, but no element of 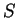 is
divisible by
is
divisible by 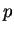 .
.
Dividing 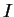 through by
through by 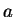 , we see that
, we see that
where
Write 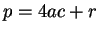 , and let
, and let
The only difference between
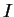
and
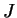
is that the endpoints of
intervals are changed by addition of an even integer.
By Lemma
2.1,
Thus
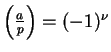
depends only on
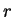
,
i.e., only on
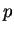
modulo
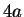
.
WOW!
If
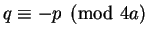 , then the only change in the above computation
is that
, then the only change in the above computation
is that 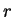 is replaced by
is replaced by 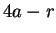 . This changes
. This changes
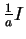 into
into
Thus
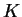
is the same as
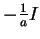
, except even integers
have been added to the endpoints. By Lemma
2.1,
so
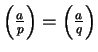
, which completes the proof.

The following more careful analysis in the special case when 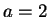 helps illustrate the proof of the above lemma, and is frequently
useful in computations.
helps illustrate the proof of the above lemma, and is frequently
useful in computations.
Proof.
When
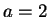
, the set
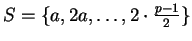
is
We must count the parity of the number of elements of
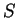
that lie in the interval
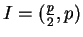
.
Writing
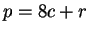
, we have
where the last equality comes from Lemma
2.1.
The possibilities for
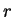
are
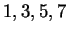
. When
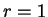
, the cardinality
is 0, when
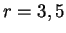
it is
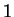
, and when
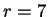
it is
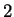
.




Next: The Quadratic Reciprocity Law
Up: Lecture 13: Quadratic Reciprocity
Previous: Recall Gauss's Lemma
William A Stein
2001-10-12
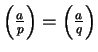 .
.
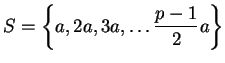
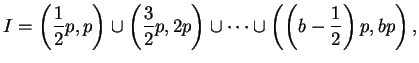
![]() through by
through by ![]() , we see that
, we see that
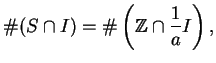
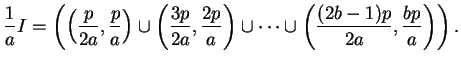
![]() , and let
, and let
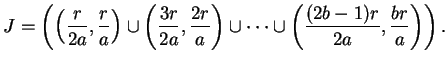
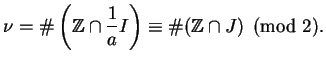
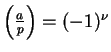 depends only on
depends only on ![]() , then the only change in the above computation
is that
, then the only change in the above computation
is that ![]() is replaced by
is replaced by ![]() . This changes
. This changes
![]() into
into
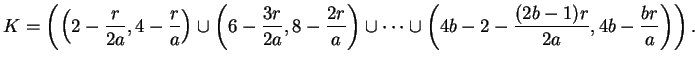
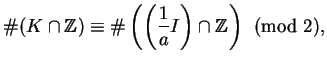
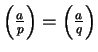 , which completes the proof.
, which completes the proof.
![]() helps illustrate the proof of the above lemma, and is frequently
useful in computations.
helps illustrate the proof of the above lemma, and is frequently
useful in computations.