


Next: Some Proofs
Up: Lecture 20: Continued Fractions
Previous: Pell's Equation
Let 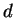 be a nonsquare positive integer, and set
be a nonsquare positive integer, and set
Then
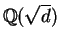 is a real quadratic field and
is a real quadratic field and
![$ \mathbb{Z}[\sqrt{d}]$](img26.png) is a ring.
There is a homomorphism called norm:
is a ring.
There is a homomorphism called norm:
Definition 3.1
An element
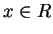
is a
unit if there exists
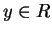
such that
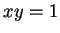
.
Proposition 3.2
The units of
![$ \mathbb{Z}[\sqrt{d}]$](img26.png)
are exactly the elements of
norm
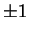
in
![$ \mathbb{Z}[\sqrt{d}]$](img26.png)
.
Proof.
Suppose
![$ u\in\mathbb{Z}[\sqrt{d}]$](img33.png)
is a unit. Then
Since
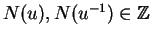
, we have
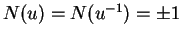

Thus Fermat's challenge amounts to determing the group 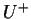 of
units in
of
units in
![$ \mathbb{Z}[\sqrt{d}]$](img26.png) of the form
of the form
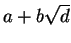 with
with
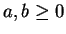 .
.
Theorem 3.3
The group
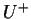
is an infinite cyclic group.
It is generated by
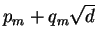
, where
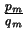
is one of the partial convergents of the
continued fraction expansion of
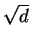
.
(In fact, if
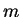
is the period of the continued fraction of
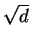
then
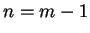
when
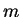
is even and
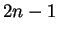
when
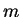
is odd.)
The theorem implies that Pell's equation always has a solution!
Warning: the smallest solution is typically shockingly large.
For example, the value of 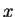 in the smallest solution to
in the smallest solution to
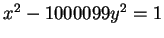 has 1118 digits.
has 1118 digits.
The following example illustrates how to use Theorem 3.3 to
solve Pell's equation when 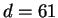 , where the simplest solution is
already quite large.
, where the simplest solution is
already quite large.
Example 3.4
Suppose
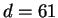
. Then
which has odd period
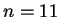
. Thus the group
is generated by
That is, we have
and
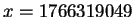
,
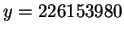
gives a solution to
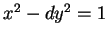
. All the other solutions arise from
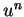
for
some
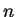
. For example,
leads to another solution.
Remark 3.5
To help with your homework, note that if the equation
has at least one (nonzero) solution
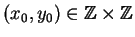
, then it
must have infinitely many solutions. This is because if
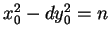
and
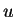
is a generator of the
cyclic group
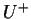
, then for any integer
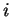
,
so
provides another solution to
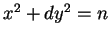
.



Next: Some Proofs
Up: Lecture 20: Continued Fractions
Previous: Pell's Equation
William A Stein
2001-10-29
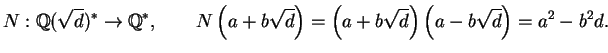
![]() of
units in
of
units in
![]() of the form
of the form
![]() with
with
![]() .
.
![]() in the smallest solution to
in the smallest solution to
![]() has 1118 digits.
has 1118 digits.
![]() , where the simplest solution is
already quite large.
, where the simplest solution is
already quite large.