


Next: Discriminants
Up: Lecture 22: Binary Quadratic
Previous: Introduction
Definition 2.1
The modular group
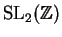
is the group of all
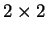
integer matrices with determinant
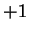
.
If
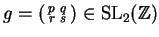 and
and
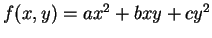 is a quadratic form, let
where for simplicity we will sometimes write
is a quadratic form, let
where for simplicity we will sometimes write
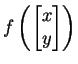 for
for 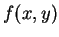 .
.
Proposition 2.2
The above formula defines a right action of the group
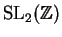
on the set of binary quadratic forms, in the sense that
Proof.

Proposition 2.3
Let
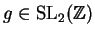
and let
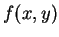
be a binary quadratic form.
The set of integers represented by
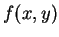
is exactly the same
as the set of integers represented by
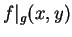
.
Proof.
If
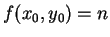
then
since
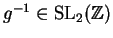
, we have
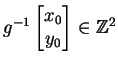
, so
Thus every integer represented by
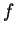
is also represented by
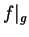
.
Conversely, if
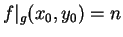
, then
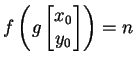
,
so
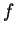
represents
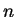
.

Define an equivalence relation 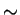 on the set of all binary
quadratic forms by declaring that
on the set of all binary
quadratic forms by declaring that 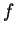 is equivalent to
is equivalent to 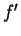 if
there exists
if
there exists
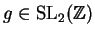 such that
such that 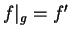 .
.
For simplicity, we will sometimes denote the quadratic form
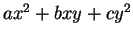 by
by 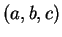 .
Then, for example, since
.
Then, for example, since
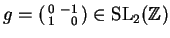 ,
we see that
,
we see that
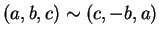 ,
since if
,
since if
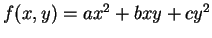 , then
, then
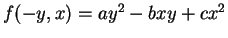 .
.
Example 2.4
Consider the binary quadratic form
Solving the representation problem for
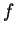
might, at first glance,
look hopeless. We find
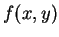
for a few values of
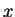
and
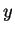
:
Each number is a sum of two squares!
Letting
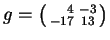
, we have
By Proposition
2.3,
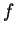
represents an integer
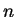
if and only if
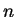
is a sum of two squares.



Next: Discriminants
Up: Lecture 22: Binary Quadratic
Previous: Introduction
William A Stein
2001-11-04
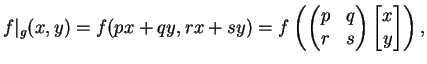
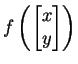 for
for 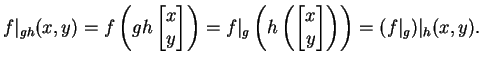
 , so
, so
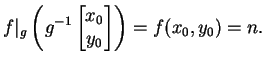
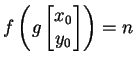 ,
so
,
so ![]() on the set of all binary
quadratic forms by declaring that
on the set of all binary
quadratic forms by declaring that ![]() is equivalent to
is equivalent to ![]() if
there exists
if
there exists
![]() such that
such that ![]() .
.
![]() by
by ![]() .
Then, for example, since
.
Then, for example, since
![]() ,
we see that
,
we see that
![]() ,
since if
,
since if
![]() , then
, then
![]() .
.