Enumerating Primes

The Sieve of Eratosthenes is an efficient way to enumerate all primes up to $n$ . The sieve works by first writing down all numbers up to $n$ , noting that $2$ is prime, and crossing off all multiples of $2$ . Next, note that the first number not crossed off is $3$ , which is prime, and cross off all multiples of $3$ , etc. Repeating this process, we obtain a list of the primes up to $n$ . Formally, the algorithm is as follows:

Algorithm 1.2 (Sieve of Eratosthenes)   Given a positive integer $n$ , this algorithm computes a list of the primes up to $n$ .

1. [Initialize] Let $X=[3,5,\ldots]$ be the list of all odd integers between $3$ and $n$ . Let $P=[2]$ be the list of primes found so far.
2. [Finished?] Let $p$ be the first element of $X$ . If $p\geq \sqrt{n}$ , append each element of $X$ to $P$ and terminate. Otherwise append $p$ to $P$ .
3. [Cross Off] Set $X$ equal to the sublist of elements in $X$ that are not divisible by $p$ . Go to step 2.

For example, to list the primes $\leq 40$ using the sieve, we proceed as follows. First $P=[2]$ and

$$X = [3,5,7,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39].$$

We append $3$ to $P$ and cross off all multiples of $3$ to obtain the new list

$$X = [5,7,11,13,17,19,23,25,29,31,35,37].$$

Next we append $5$ to $P$ , obtaining $P=[2,3,5]$ , and cross off the multiples of $5$ , to obtain $X = [7,11,13,17,19,23,29,31,37].$ Because $7^2\geq 40$ , we append $X$ to $P$ and find that the primes less than $40$ are

$$2,3,5, 7,11,13,17,19,23,29,31,37.$$

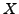
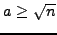
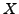
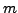
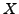
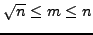
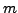
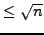
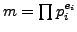
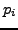
Proof. [Proof of Algorithm 1.2.3] The part of the algorithm that is not clear is that when the first element $a$ of $X$ satisfies $a\geq \sqrt{n}$ , then each element of $X$ is prime. To see this, suppose $m$ is in $X$ , so $\sqrt{n} \leq m\leq n$ and that $m$ is divisible by no prime that is $\leq \sqrt{n}$ . Write $m=\prod p_i^{e_i}$ with the $p_i$ distinct primes ordered so that $p_1<p_2<\ldots$ . 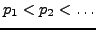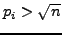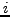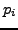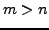If $p_i>\sqrt{n}$ for each $i$ and there is more than one $p_i$ , then $m>n$ , a contradiction. 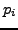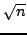Thus some $p_i$ is less than $\sqrt{n}$ , which also contradicts our assumptions on $m$ . $\qedsymbol$

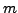
SAGE Example 1.2   The eratosthenes command implements the sieve in SAGE:

sage: eratosthenes(50)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]