Index

$\left(\frac{a}{p}\right)$

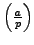
nn

abelian group

nn

algebraic number

nn

algorithm

nn

Chinese Remainder Theorem

The Chinese Remainder Theorem

Compute Power

How to Compute $a^m\pmod{n}$

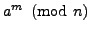
Division Algorithm

The Greatest Common Divisor

Elliptic Curve Factorization Method

Lenstra's Elliptic Curve Factorization

Elliptic Curve Group Law

The Group Structure on

Extended Euclidean Algorithm

How to Solve $ax\equiv 1\pmod{n}$

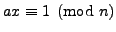
Greatest Common Division

The Greatest Common Divisor

Inverse Modulo $n$

How to Solve $ax\equiv 1\pmod{n}$

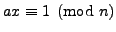
Least Common Multiple of First 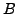$B$ Integers

Pollard's 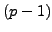$(p-1)$ -Method

Miller-Rabin Primality Test

Primality Testing

Pollard 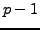$p-1$ Method

Pollard's 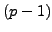$(p-1)$ -Method

Primitive Root

Computing Primitive Roots

Probabilistic Algorithm to Factor $n$

Factoring $n$ Given $d$

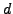
Sieve of Eratosthenes

Enumerating Primes

Write a number in binary

How to Compute $a^m\pmod{n}$

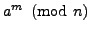
Artin

Artin's Conjecture

Artin's conjecture

nn

binary, writing number in

How to Compute $a^m\pmod{n}$

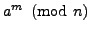
cancellation proposition

Linear Equations Modulo $n$

Carmichael numbers

nn

Certicom challenges

The Elliptic Curve Discrete

Chinese remainder theorem

The Chinese Remainder Theorem | The Chinese Remainder Theorem

commutative ring

nn

complete set of residues

nn | Linear Equations Modulo $n$

composite

nn

compute

continued fraction

Infinite Continued Fractions

gcd

The Greatest Common Divisor

greatest common divisor

The Greatest Common Divisor

inverse modulo $n$

Quickly Computing Inverses and

powers modulo $n$

Quickly Computing Inverses and

powers modulo $n$

nn

square roots mod $p$

Finding Square Roots

square roots mod $p$

to Finding Square Roots

congruences

Congruences Modulo $n$

congruent number

nn | nn

157 is

The Congruent Number Problem

all 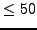$\leq 50$ are

The Congruent Number Problem

and arithmetic progression

The Congruent Number Problem

and elliptic curves

The Congruent Number Problem

problem

The Congruent Number Problem

why called congruent

The Congruent Number Problem

congruent number criterion proposition

The Congruent Number Problem

congruent numbers and elliptic curves proposition

The Congruent Number Problem

conjecture

Artin

nn

continued fraction

nn | Continued Fractions | Sums of Two Squares | Sums of Two Squares to Exercises

algorithm

The Continued Fraction Procedure

convergents

The Sequence of Partial

every rational number has

Every Rational Number is

of $e$

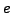
The Continued Fraction Procedure

of $e$

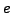
nn

of $\sqrt{2}$

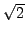
Quadratic Irrationals

of $\sqrt[3]{2}$

Continued Fractions of Algebraic

of algebraic number

Continued Fractions of Algebraic

of finite length

nn

of higher degree number

Continued Fractions of Algebraic

of quadratic irrational

Quadratic Irrationals

partial convergents of

nn

periodic

nn

recognizing rational numbers

nn

continued fraction convergence theorem

Convergence of Infinite Continued

continued fraction existence theorem

Convergence of Infinite Continued

continued fraction limit theorem

Convergence of Infinite Continued

continued fraction procedure

Convergence of Infinite Continued

continued fraction process

nn

convergence of continued fraction proposition

Convergence of Infinite Continued

convergent

nn

convergents

partial

The Sequence of Partial

convergents in lowest terms corollary

Partial Convergents

corollary

convergents in lowest terms

Partial Convergents

cryptography

The Largest Known Prime

using elliptic curves

Elliptic Curve Cryptography

cryptosystem

Diffie-Hellman

Public-Key Cryptography | nn

ElGamal

The ElGamal Cryptosystem and | The ElGamal Cryptosystem and | The ElGamal Cryptosystem and

RSA

The RSA Cryptosystem to Factoring $n$ Given $d$

decryption key proposition

How RSA works

density of primes

How Many Primes are

deterministic primality test

Primality Testing

Diffie-Hellman cryptosystem

Public-Key Cryptography | nn

on elliptic curve

Elliptic Curve Analogues of

digital signatures

The Man in the

Dirichlet theorem

Primes of the Form

discrete log problem

The Discrete Log Problem | The Discrete Log Problem

difficulty of

The Discrete Log Problem

on elliptic curve

Elliptic Curve Analogues of | The Elliptic Curve Discrete

divides

nn | Primes

divisibility by 3 proposition

Congruences Modulo $n$

divisibility tests

Congruences Modulo $n$

division algorithm

The Greatest Common Divisor

divisor

nn

does not divide

nn

ECM

Integer Factorization Using Elliptic | Integer Factorization Using Elliptic

ElGamal cryptosystem

The ElGamal Cryptosystem and | The ElGamal Cryptosystem and

elliptic curve

nn

and congruent numbers

The Congruent Number Problem

cryptography

Elliptic Curve Cryptography

Diffie-Hellman

Elliptic Curve Analogues of

discrete log problem

Elliptic Curve Analogues of | The Elliptic Curve Discrete

factorization

Integer Factorization Using Elliptic | nn

group structure

nn

rank

The Torsion Subgroup of

rational points on

Elliptic Curves Over the

torsion subgroup

The Torsion Subgroup of

elliptic curve discrete log problem

nn

elliptic curve group law theorem

The Group Structure on

equivalence relation

congruence modulo $n$

Congruences Modulo $n$

Euclid

Prime Numbers

Euclid theorem

The Greatest Common Divisor

Euclid's theorem

on divisibility

The Greatest Common Divisor

Euler

Euler's Criterion | The Continued Fraction of

phi function

Congruences Modulo $n$ | Fermat's Little Theorem | Multiplicative Functions

is multiplicative

Multiplicative Functions

Euler proposition

Euler's Proposition

Euler's criterion proposition

Euler's Criterion

Euler's proposition

Euler's Proposition

extended Euclidean algorithm

How to Solve $ax\equiv 1\pmod{n}$

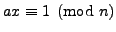
extended Euclidean proposition

How to Solve $ax\equiv 1\pmod{n}$

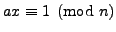
factorization

and breaking RSA

Factoring $n$ Given | Factoring $n$ Given $d$

difficulty of

Numbers Factor as Products

Pollard's $(p-1)$ -method

Pollard's $(p-1)$ -Method

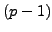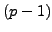Pollard's $(p-1)$ -method

to Pollard's 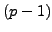$(p-1)$ -Method

quantum

Numbers Factor as Products

using elliptic curves

Integer Factorization Using Elliptic

Fermat factorization method

nn

Fermat's little theorem

Fermat's Little Theorem | Fermat's Little Theorem

group-theoretic interpretation

Fermat's Little Theorem

field

nn

of integers modulo $p$

Congruences Modulo $n$

of integers modulo $p$

Exercises

finite continued fraction

nn | nn

finite field

Congruences Modulo $n$

floor

nn

fundamental theorem of arithmetic

Primes | The Greatest Common Divisor | The Fundamental Theorem of

Gauss

How Many Primes are | Quadratic Reciprocity | Statement of the Quadratic | Statement of the Quadratic | Statement of the Quadratic | First Proof of Quadratic | First Proof of Quadratic

Gauss sum

nn

Gauss sum proposition

A Proof of Quadratic

Gauss's lemma

First Proof of Quadratic

gcd

The Greatest Common Divisor

gcd algorithm

The Greatest Common Divisor

Generalized Riemann Hypothesis

nn

geometric group law proposition

The Group Structure on

greatest common divisor

The Greatest Common Divisor

group

Congruences Modulo $n$

$(\mathbb{Z}/m\mathbb{Z}{})^*$

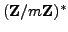
Fermat's Little Theorem

of units

Congruences Modulo $n$

structure of elliptic curve

nn

group homomorphism

nn

Hadamard

How Many Primes are

homomorphism of rings

nn

Hooley

Artin's Conjecture

how convergents converge proposition

The Sequence of Partial

infinitely many primes proposition

Primes of the Form

infinitely many primes theorem

There Are Infinitely Many

infinitely many triangles theorem

The Congruent Number Problem

injective

nn

integers

Primes

factor

Numbers Factor as Products

factor uniquely

Primes | The Fundamental Theorem of

modulo $n$

Congruences Modulo $n$

isomorphism

nn

joke

There Are Infinitely Many

kernel

nn

Lagrange

Wilson's Theorem

Lang

Continued Fractions of Algebraic

largest known

elliptic curve rank

The Torsion Subgroup of

prime

The Largest Known Prime

value of $\pi(x)$

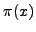
How Many Primes are

Legendre Symbol

nn

Legendre symbol of 2 proposition

Euler's Proposition

Lenstra

There Are Infinitely Many | Integer Factorization Using Elliptic to Motivation for the Elliptic

lift

nn

long division proposition

The Greatest Common Divisor

man in the middle attack

nn

Mazur theorem

The Torsion Subgroup of

Mersenne prime

nn

Michael

to The Man in the | Elliptic Curve Analogues of | The ElGamal Cryptosystem and

modular arithmetic

and linear equations

Linear Equations Modulo $n$

order of element

Fermat's Little Theorem

Mordell

Elliptic Curves Over the | Elliptic Curves Over the

Mordell theorem

Elliptic Curves Over the

multiplicative

nn

functions

Multiplicative Functions

order

Congruences Modulo $n$

multiplicative of Euler's function proposition

Multiplicative Functions

natural numbers

Primes

Nikita

to Attacking RSA | Elliptic Curve Analogues of | The ElGamal Cryptosystem and

normal

nn

notation

Preface

number of primitive roots proposition

Existence of Primitive Roots

one-way function

nn

open problem

congruent numbers

The Congruent Number Problem

decide if congruent number

The Congruent Number Problem

fast integer factorization

Numbers Factor as Products

order

nn | nn

of element

Fermat's Little Theorem

partial convergents

nn | nn

partial convergents proposition

Partial Convergents

period continued fraction theorem

Periodic Continued Fractions

period of the continued fraction

nn

periodic continued fraction

nn | nn

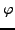$\varphi$ function

Congruences Modulo $n$

phi function

is multiplicative

Multiplicative Functions

Pieter

Artin's Conjecture

polynomial time

nn

polynomials

over $\mathbb{Z}/p\mathbb{Z}{}$

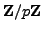
Polynomials over $\mathbb{Z}/p\mathbb{Z}{}$

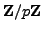
power smooth

nn

powering algorithm

nn

primality test

deterministic

Primality Testing

Miller-Rabin

Primality Testing

probabilistic

Quickly Computing Inverses and

pseudoprime

Primality Testing

prime

nn

prime factorization proposition

Numbers Factor as Products

prime number theorem

The Sequence of Prime | How Many Primes are

primes

Prime Numbers

density of

How Many Primes are

infinitely many

There Are Infinitely Many

largest known

The Largest Known Prime

Mersenne

The Largest Known Prime

of form $ax+b$

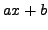
Primes of the Form

of form $4x-1$

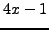
Primes of the Form

of the form $6x-1$

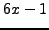
Exercises

sequence of

The Sequence of Prime

testing for

Primality Testing

primitive

nn | nn

representation

Sums of Two Squares

primitive root

nn

existence

Existence of Primitive Roots

mod power of two

The Structure of $(\mathbb{Z}/p\mathbb{Z}{})^*$

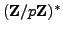
primitive root mod prime powers theorem

Existence of Primitive Roots

primitive root of unity

nn

primitive root theorem

Existence of Primitive Roots

proposition

cancellation

Linear Equations Modulo $n$

congruent number criterion

The Congruent Number Problem

congruent numbers and elliptic curves

The Congruent Number Problem

convergence of continued fraction

Convergence of Infinite Continued

decryption key

How RSA works

divisibility by 3

Congruences Modulo $n$

Euler

Euler's Proposition

Euler's criterion

Euler's Criterion

extended Euclidean

How to Solve $ax\equiv 1\pmod{n}$

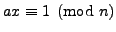
Gauss sum

A Proof of Quadratic

geometric group law

The Group Structure on

how convergents converge

The Sequence of Partial

infinitely many primes

Primes of the Form

Legendre symbol of 2

Euler's Proposition

long division

The Greatest Common Divisor

multiplicative of Euler's function

Multiplicative Functions

number of primitive roots

Existence of Primitive Roots

partial convergents

Partial Convergents

prime factorization

Numbers Factor as Products

rational continued fractions

Every Rational Number is

root bound

Polynomials over $\mathbb{Z}/p\mathbb{Z}{}$

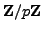
solvability

Linear Equations Modulo $n$

units

Linear Equations Modulo $n$

Wilson

Wilson's Theorem

Pseudoprimality theorem

Primality Testing

pseudoprime

nn

public key

nn

quadratic irrational

nn

continued fraction of

Quadratic Irrationals

quadratic nonresidue

nn

quadratic reciprocity

Quadratic Reciprocity

elementary proof

First Proof of Quadratic to Proof of Quadratic Reciprocity

Gauss sums proof

A Proof of Quadratic

quadratic reciprocity theorem

Statement of the Quadratic

quadratic residue

nn | nn

quantum computer

Numbers Factor as Products | The Discrete Log Problem

rank

The Torsion Subgroup of | nn

rational continued fractions proposition

Every Rational Number is

rational point

nn

recognizing rational numbers

nn

Riemann Hypothesis

The Sequence of Prime | How Many Primes are | How Many Primes are

bound on $\pi(x)$

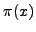
How Many Primes are

ring

nn

root bound proposition

Polynomials over $\mathbb{Z}/p\mathbb{Z}{}$

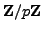
root of unity

nn | nn

primitive

nn

RSA cryptosystem

The RSA Cryptosystem to Factoring $n$ Given $d$

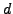
RSA-155

Numbers Factor as Products

RSA-576

Numbers Factor as Products

Shor

Numbers Factor as Products | The Discrete Log Problem

simple continued fraction

nn

smooth

nn

solvability proposition

Linear Equations Modulo $n$

square roots

how to find mod $p$

Finding Square Roots

how to find mod $p$

to Finding Square Roots

squares

sum of two

Sums of Two Squares

subgroup

nn

sum of two squares theorem

Sums of Two Squares

sums of two squares

Sums of Two Squares

surjective

nn

table

comparing 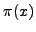$\pi(x)$ to $x/(\log(x)-1)$

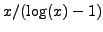
How Many Primes are

values of $\pi(x)$

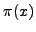
How Many Primes are

when 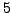$5$ a square mod $p$

Statement of the Quadratic

The Man

The Man in the

theorem

Chinese remainder

The Chinese Remainder Theorem

continued fraction convergence

Convergence of Infinite Continued

continued fraction existence

Convergence of Infinite Continued

continued fraction limit

Convergence of Infinite Continued

Dirichlet

Primes of the Form

elliptic curve group law

The Group Structure on

Euclid

The Greatest Common Divisor

Fermat's little

Fermat's Little Theorem | Fermat's Little Theorem

infinitely many primes

There Are Infinitely Many

infinitely many triangles

The Congruent Number Problem

Mazur

The Torsion Subgroup of

Mordell

Elliptic Curves Over the

of Dirichlet

The Sequence of Prime

of Wilson

Wilson's Theorem

period continued fraction

Periodic Continued Fractions

prime number

How Many Primes are

primitive root

Existence of Primitive Roots

primitive root mod prime powers

Existence of Primitive Roots

Pseudoprimality

Primality Testing

quadratic reciprocity

Statement of the Quadratic

sum of two squares

Sums of Two Squares

unique factorization

Primes

torsion subgroup

The Torsion Subgroup of

Trotter

Continued Fractions of Algebraic

unique factorization

Primes

unique factorization theorem

Primes

unit group

Congruences Modulo $n$

units

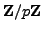of $\mathbb{Z}/p\mathbb{Z}{}$ are cyclic

nn

roots of unity

nn

units proposition

Linear Equations Modulo $n$

Vallée Poussin

How Many Primes are

Wilson proposition

Wilson's Theorem

Wilson's theorem

Wilson's Theorem

Zagier

The Congruent Number Problem