Linear Equations Modulo 
In this section, we
are concerned with how to decide whether or not a linear equation of
the form
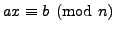 has a solution modulo
has a solution modulo  .
Algorithms for computing solutions to
.
Algorithms for computing solutions to
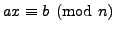 are the topic of Section 2.3.
are the topic of Section 2.3.
First we prove a proposition that gives a criterion under
which one can cancel a quantity from both sides of a congruence.
Proof.
By definition
Since
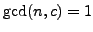
, it follows
from Theorem
1.1.6 that
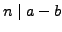
, so
as claimed.

When  has a multiplicative inverse
has a multiplicative inverse 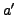 in
in
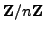 (i.e.,
(i.e.,
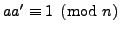 ) then the equation
) then the equation
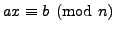 has a unique
solution
has a unique
solution
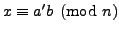 modulo
modulo  . Thus, it is of interest to
determine the units in
. Thus, it is of interest to
determine the units in
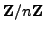 , i.e., the elements which have a
multiplicative inverse.
, i.e., the elements which have a
multiplicative inverse.
We will use complete sets of residues
to prove that the units in
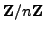 are exactly the
are exactly the
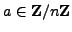 such that
such that
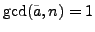 for any lift
for any lift 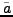 of
of  to
to
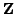 (it doesn't matter which lift).
(it doesn't matter which lift).
Definition 2.1 (Complete Set of Residues)
We call a subset
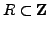
of size

whose reductions modulo

are
pairwise distinct a
complete set of residues
modulo

. In other words, a complete set of residues is a choice of
representative for each equivalence class in
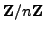
.
For example,
is a complete set of residues modulo  .
When
.
When 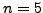 ,
,
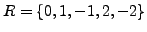 is a complete set of residues.
is a complete set of residues.
Lemma 2.1
If 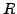 is a complete set of residues modulo
is a complete set of residues modulo  and
and
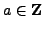 with
with
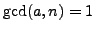 , then
, then
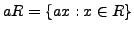 is also a complete set of residues modulo
is also a complete set of residues modulo  .
.
Proof.
If
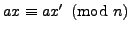
with
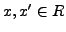
, then
Proposition
2.1.9 implies that
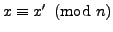
.
Because
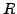
is a complete set of residues, this implies
that
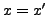
. Thus the elements of
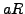
have distinct reductions modulo

.
It follows, since
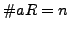
, that
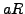
is a
complete set of residues modulo

.

Proof.
Let
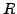
be a complete set of residues modulo

, so there
is a unique element of
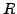
that is congruent to
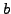
modulo

.
By Lemma
2.1.11,
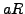
is also a complete set of residues modulo

, so
there is a unique element
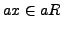
that is congruent
to
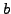
modulo

, and we have
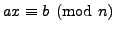
.

Algebraically, this proposition asserts that if
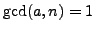 , then
the map
, then
the map
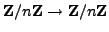 given by left multiplication by
given by left multiplication by  is
a bijection.
is
a bijection.
Example 2.1
Consider the equation

,
and the complete set
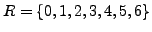
of coset representatives. We have
so
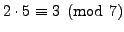
.
When
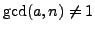 , then the equation
, then the equation
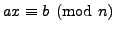 may or
may not have a solution. For example,
may or
may not have a solution. For example,
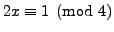 has no
solution, but
has no
solution, but
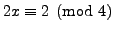 does, and in fact it has more than
one mod
does, and in fact it has more than
one mod 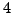 (
(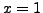 and
and 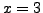 ). Generalizing
Proposition 2.1.12, we obtain the following more general
criterion for solvability.
). Generalizing
Proposition 2.1.12, we obtain the following more general
criterion for solvability.
Proof.
Let
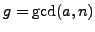
. If there is a solution
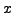
to the equation
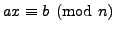
, then
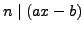
. Since
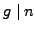
and
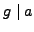
, it follows that
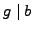
.
Conversely, suppose that 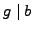 . Then
. Then
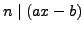 if and only
if
if and only
if
Thus
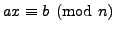
has a solution if and only if
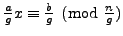
has a solution. Since
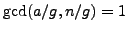
, Proposition
2.1.12 implies this
latter equation does have a solution.

In Chapter 4 we will study quadratic reciprocity,
which gives a nice criterion for whether or not a quadratic equation
modulo  has a solution.
has a solution.
William
2007-06-01
![]() has a multiplicative inverse
has a multiplicative inverse ![]() in
in
![]() (i.e.,
(i.e.,
![]() ) then the equation
) then the equation
![]() has a unique
solution
has a unique
solution
![]() modulo
modulo ![]() . Thus, it is of interest to
determine the units in
. Thus, it is of interest to
determine the units in
![]() , i.e., the elements which have a
multiplicative inverse.
, i.e., the elements which have a
multiplicative inverse.
![]() are exactly the
are exactly the
![]() such that
such that
![]() for any lift
for any lift ![]() of
of ![]() to
to
![]() (it doesn't matter which lift).
(it doesn't matter which lift).
![]() , then the equation
, then the equation
![]() may or
may not have a solution. For example,
may or
may not have a solution. For example,
![]() has no
solution, but
has no
solution, but
![]() does, and in fact it has more than
one mod
does, and in fact it has more than
one mod ![]() (
(![]() and
and ![]() ). Generalizing
Proposition 2.1.12, we obtain the following more general
criterion for solvability.
). Generalizing
Proposition 2.1.12, we obtain the following more general
criterion for solvability.
![]() . Then
. Then
![]() if and only
if
if and only
if 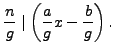
![]() has a solution.
has a solution.