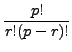2..
- Prove that for any positive
integer
 , the set
, the set
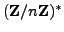 under multiplication
modulo
under multiplication
modulo  is a group.
is a group.
- Compute the following gcd's using
Algorithm 1.1.13:
-
Use Algorithm 2.3.7 to find
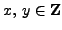 such that
such that
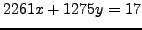 .
.
-
Prove that if
 and
and 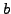 are integers and
are integers and  is a prime,
then
is a prime,
then
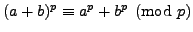 . You may assume
that the binomial coefficient
. You may assume
that the binomial coefficient
is an integer.
-
- Prove that if
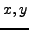 is a solution to
is a solution to
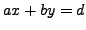 ,
then for all
,
then for all
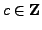 ,
,
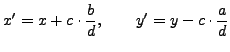 |
(2.6.1) |
is also a solution to 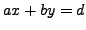 .
.
- Find two distinct solutions to
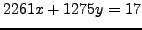 .
.
- Prove that all solutions are of the form (2.6.1)
for some
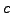 .
.
- Let
![$ f(x)=x^2+ax+b \in\mathbb{Z}[x]$](img896.png) be a quadratic
polynomial with integer coefficients
and positive leading coefficients, e.g.,
be a quadratic
polynomial with integer coefficients
and positive leading coefficients, e.g.,
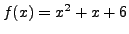 .
Formulate a conjecture about when the set
.
Formulate a conjecture about when the set
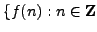 and $f(n)$ is prime
and $f(n)$ is prime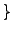 is infinite. Give numerical evidence
that supports your conjecture.
is infinite. Give numerical evidence
that supports your conjecture.
-
Find four complete sets of residues modulo
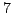 , where the
, where the
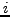 th set satisfies the
th set satisfies the 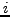 th condition:
(1) nonnegative, (2) odd, (3) even, (4) prime.
th condition:
(1) nonnegative, (2) odd, (3) even, (4) prime.
-
Find rules in the spirit of
Proposition 2.1.8 for divisibility of an integer
by
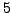 ,
, 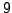 , and
, and 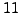 , and prove each of these rules using
arithmetic modulo a suitable
, and prove each of these rules using
arithmetic modulo a suitable  .
.
- (*)The following problem is from the 1998 Putnam Competition. Define a
sequence of decimal integers
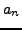 as follows:
as follows: 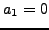 ,
, 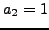 , and
, and
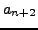 is obtained by writing the digits of
is obtained by writing the digits of 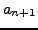 immediately
followed by those of
immediately
followed by those of 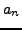 . For example,
. For example, 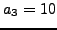 ,
, 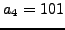 ,
and
,
and
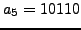 .
Determine the
.
Determine the  such that
such that 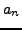 a multiple of
a multiple of 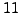 , as follows:
, as follows:
- Find the smallest integer
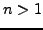 such that
such that 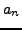 is divisible by
is divisible by
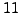 .
.
- Prove that
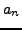 is divisible by
is divisible by 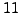 if and only if
if and only if
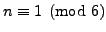 .
.
- Find an integer
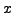 such that
such that
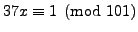 .
.
- What is the order of
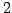 modulo
modulo 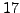 ?
?
-
Let
 be a prime. Prove that
be a prime. Prove that
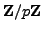 is a field.
is a field.
- Find an
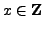 such that
such that
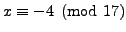 and
and
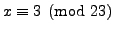 .
.
- Prove that if
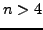 is composite then
is composite then
- For what values of
 is
is
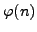 odd?
odd?
-
- Prove that
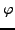 is multiplicative as follows. Suppose
is multiplicative as follows. Suppose 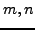 are
positive integers and
are
positive integers and
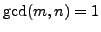 . Show that
the natural map
. Show that
the natural map
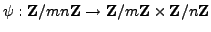 is
an injective homomorphism of rings, hence bijective by counting, then
look at unit groups.
is
an injective homomorphism of rings, hence bijective by counting, then
look at unit groups.
- Prove conversely that if
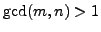 then
the natural map
then
the natural map
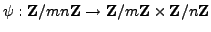 is not an isomorphism.
is not an isomorphism.
- Seven competitive math students try to
share a huge hoard of stolen math books equally between themselves.
Unfortunately, six books are left over, and in the fight over them,
one math student is expelled. The remaining six math students,
still unable to share the math books equally since two are left
over, again fight, and another is expelled. When the remaining five
share the books, one book is left over, and it is only after yet
another math student is expelled that an equal sharing is possible.
What is the minimum number of books which allow this to happen?
- Show that if
 is a positive integer such that both
is a positive integer such that both  and
and 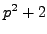 are prime, then
are prime, then 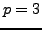 .
.
- Let
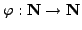 be the
Euler
be the
Euler 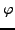 function.
function.
- Find all natural numbers
 such that
such that
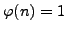 .
.
- Do there exist natural numbers
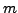 and
and  such that
such that
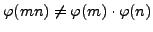 ?
?
- Find a formula for
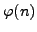 directly in terms
of the prime factorization of
directly in terms
of the prime factorization of  .
.
-
- Prove that if
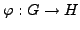 is a group
homomorphism, then
is a group
homomorphism, then
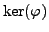 is a subgroup of
is a subgroup of 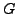 .
.
- Prove that
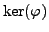 is normal, i.e., that
if
is normal, i.e., that
if 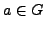 and
and
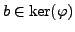 , then
, then
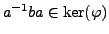 .
.
- Is the set
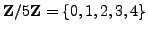 with binary operation
multiplication modulo
with binary operation
multiplication modulo 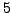 a group?
a group?
- Find all four solutions to the equation
-
Prove that for any positive integer
 the fraction
the fraction
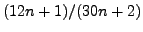 is in reduced form.
is in reduced form.
- Suppose
 and
and 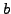 are positive integers.
are positive integers.
- Prove that
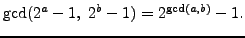
- Does it matter if
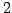 is replaced by an arbitrary prime
is replaced by an arbitrary prime  ?
?
- What if
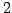 is replaced by an arbitrary positive integer
is replaced by an arbitrary positive integer  ?
?
- For every positive integer
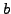 , show that there exists a positive
integer
, show that there exists a positive
integer  such that the polynomial
such that the polynomial
![$ x^2-1\in(\mathbb{Z}/n\mathbb{Z}{})[x]$](img929.png) has at least
has at least 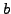 roots.
roots.
-
- Prove that there is no primitive root
modulo
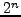 for any
for any 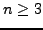 .
.
- (*) Prove that
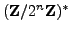 is generated by
is generated by 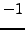 and
and 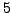 .
.
- Let
 be an odd prime.
be an odd prime.
- (*) Prove that there is a primitive root modulo
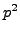 .
(Hint: Use that if
.
(Hint: Use that if 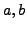 have orders
have orders 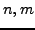 , with
, with
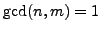 , then
, then 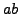 has order
has order 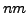 .)
.)
- Prove that for any
 , there is a primitive root modulo
, there is a primitive root modulo 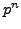 .
.
- Explicitly find a primitive root modulo
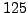 .
.
- (*)
In terms of the prime factorization of
 , characterize the
integers
, characterize the
integers  such that there is a primitive root modulo
such that there is a primitive root modulo  .
.
- Compute the last two digits
of
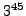 .
.
- Find the integer
 such that
such that
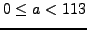 and
and
- Find the proportion of primes
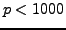 such that
such that 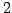 is a primitive root modulo
is a primitive root modulo  .
.
- Find a prime
 such that the smallest
primitive root modulo
such that the smallest
primitive root modulo  is
is 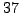 .
.
William
2007-06-01