First Proof of Quadratic Reciprocity

Our first proof of quadratic reciprocity is elementary. The proof involves keeping track of integer points in intervals. Proving Gauss's lemma is the first step; this lemma computes $\left(\frac{a}{p}\right)$ in terms of the number of integers of a certain type that lie in a certain interval. Next we prove Lemma 4.3.3, which controls how the parity of the number of integer points in an interval changes when an endpoint of the interval is changed. Then we prove that $\left(\frac{a}{p}\right)$ depends only on $p$ modulo $4a$ by applying Gauss's lemma and keeping careful track of intervals as they are rescaled and their endpoints are changed. Finally, in Section 4.3.2 we use some basic algebra to deduce the quadratic reciprocity law using the tools we've just developed. Our proof follows the one given in [#!davenport!#] closely.

Lemma 4.3 (Gauss's Lemma)   Let $p$ be an odd prime and let $a$ be an integer $\not\equiv 0\pmod{p}$ . Form the numbers

$$a, 2a, 3a, \ldots, \frac{p-1}{2} a$$

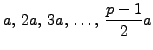
and reduce them modulo $p$ to lie in the interval $(-\frac{p}{2}, \frac{p}{2})$ , i.e., for each of the above numbers $ka$ find a number in the interval $(-\frac{p}{2}, \frac{p}{2})$ that is congruent to $ka$ modulo $p$ . Let $\nu$ be the number of negative numbers in the resulting set. Then

$$\left(\frac{a}{p}\right) = (-1)^{\nu}.$$

Proof. In defining $\nu$ , we expressed each number in

$$S = \left\{a, 2a, \ldots, \frac{p-1}{2} a\right\}$$

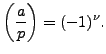
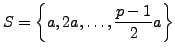
as congruent to a number in the set

$$\left\{ 1, -1, 2, -2, \ldots, \frac{p-1}{2}, -\frac{p-1}{2}\right\}.$$

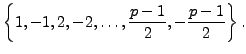
No number $1, 2, \ldots, \frac{p-1}{2}$ appears more than once, with either choice of sign, because if it did then either two elements of $S$ are congruent modulo $p$ or 0 is the sum of two elements of $S$ , and both events are impossible (the former case cannot occur because of cancellation modulo $p$ , and in the latter case we would have that $ka + ja \equiv 0 \pmod{p}$ for $1\leq k,j \leq (p-1)/2$ , so $k+j\equiv 0\pmod{p}$ , a contradiction). Thus the resulting set must be of the form

$$T = \left\{\varepsilon _1\cdot 1, \varepsilon _2 \cdot 2, \ldots, \varepsilon _{(p-1)/2}\cdot \frac{p-1}{2} \right\},$$

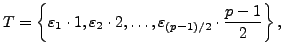
where each $\varepsilon _i$ is either $+1$ or $-1$ . Multiplying together the elements of $S$ and of $T$ , we see that

$$(1a) \cdot (2a)\cdot(3a) \cdots \left(\frac{p-1}{2} a\right) \equiv$$

$$(\varepsilon _1\cdot 1)\cdot (\varepsilon _2 \cdot 2) \cdots \left(\varepsilon _{(p-1)/2} \cdot \frac{p-1}{2}\right)\pmod{p},$$

so

$$a^{(p-1)/2} \equiv \varepsilon _1\cdot \varepsilon _2 \cdots \varepsilon _{(p-1)/2}\pmod{p}.$$

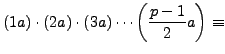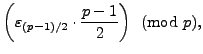The lemma then follows from Proposition 4.2.1, since $\left(\frac{a}{p}\right) = a^{(p-1)/2}$ . $\qedsymbol$

SAGE Example 4.3   We illustrate Gauss's lemma using SAGE. The function gauss below prints out a list of the normalized numbers appearing in the statement of Gauss's lemma, and returns $(-1)^{\nu}$ . In each case below, $(-1)^{\nu} = \left(\frac{a}{p}\right)$ .

sage: def gauss(a, p):
...    # make the list of numbers reduced modulo p
...    v = [(n*a)%p for n in range(1, (p-1)//2 + 1)]
...    # normalize them to be in the range -p/2 to p/2
...    v = [(x if (x < p/2) else x - p) for x in v]
...    # sort and print the resulting numbers
...    v.sort()
...    print v
...    # count the number that are negative
...    num_neg = len([x for x in v if x < 0])
...    return (-1)^num_neg
sage: gauss(2, 13) 
[-5, -3, -1, 2, 4, 6]
-1
sage: legendre_symbol(2,13) 
-1
sage: gauss(4, 13) 
[-6, -5, -2, -1, 3, 4]
1
sage: legendre_symbol(4,13)  
1
sage: gauss(2,31) 
[-15, -13, -11, -9, -7, -5, -3, -1, 2, 4, 6, 8, 10, 12, 14]
1
sage: legendre_symbol(2,31) 
1