Finite Continued Fractions

This section is about continued fractions of the form $[a_0,a_1,\ldots, a_m]$ for some $m\geq 0$ . We give an inductive definition of numbers $p_n$ and $q_n$ such that for all $n\leq m$

$$[a_0,a_1,\ldots,a_n] = \frac{p_n}{q_n}.$$ (5.1.1)

We then give related formulas for the determinants of the $2\times 2$ matrices $\left(\begin{smallmatrix}p_n&p_{n-1} q_n&q_{n-1}\end{smallmatrix}\right)$ and $\left(\begin{smallmatrix}p_n&p_{n-2} q_n&q_{n-2}\end{smallmatrix}\right)$ . which we will repeatedly use to deduce properties of the sequence of partial convergents $[a_0,\ldots,a_k]$ . We will use Algorithm 1.1.13 to prove that every rational number is represented by a continued fraction, as in (5.1.1).

Definition 5.1 (Finite Continued Fraction)   A finite continued fraction is an expression

$$a_0 + \frac{1}{\displaystyle a_1+\frac{1}{\displaystyle a_2 + \displaystyle \frac{1}{ \cdots +\frac{1}{a_n}}}},$$

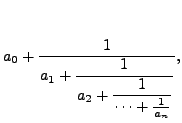
where each $a_m$ is a real number and $a_m>0$ for all $m\geq 1$ .

Definition 5.1 (Simple Continued Fraction)   A simple continued fraction is a finite or infinite continued fraction in which the $a_i$ are all integers.

To get a feeling for continued fractions, observe that

$$[a_0] = a_0,$$

$$[a_0, a_1] = a_0 + \frac{1}{a_1} = \frac{a_0 a_1 + 1}{a_1},$$

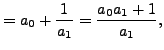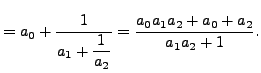$$[a_0, a_1, a_2] = a_0 + \frac{1}{a_1 +\displaystyle \frac{1}{a_2}} = \frac{a_0 a_1 a_2 + a_0 + a_2}{a_1 a_2 + 1}.$$

Also,

$$[a_0, a_1, \ldots ,a_{n-1}, a_n] = \left[a_0, a_1, \ldots, a_{n-2}, a_{n-1} + \frac{1}{a_n}\right]$$

$$= a_0 + \frac{1}{[a_1,\ldots, a_n]}$$

$$= [a_0, [a_1,\ldots, a_n]].$$

SAGE Example 5.1   The SAGE command continued_fraction computes continued fractions:

sage: continued_fraction(17/23) 
[0, 1, 2, 1, 5]
sage: continued_fraction(e) 
[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 11]

Use the optional second argument bits = n to determine the precision (in bits) of the input number that is used to compute the continued fraction.

sage: continued_fraction(e, bits=20)  
[2, 1, 2, 1, 1, 4, 1, 1, 6]
sage: continued_fraction(e, bits=30) 
[2, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1]

You can obtain the value of a continued fraction and even do arithmetic with continued fractions:

sage: a = continued_fraction(17/23); a
[0, 1, 2, 1, 5]
sage: a.value() 
17/23
sage: b = continued_fraction(6/23); b
[0, 3, 1, 5]
sage: a + b 
[1]