Numbers Factor as Products of Primes

In this section, we prove that every natural number factors as a product of primes. Then we discuss the difficulty of finding such a decomposition in practice. We will wait until Section 1.1.4 to prove that factorization is unique.

As a first example, let $n=1275$ . The sum of the digits of $n$ is divisible by $3$ , so $n$ is divisible by $3$ (see Proposition 2.1.8), and we have $n=3\cdot 425$ . The number $425$ is divisible by $5$ , since its last digit is $5$ , and we have $1275 = 3\cdot 5 \cdot 85$ . Again, dividing $85$ by $5$ , we have $1275 = 3\cdot 5^2 \cdot 17$ , which is the prime factorization of $1275$ . Generalizing this process proves the following proposition:

Proposition 1.1   Every natural number is a product of primes.

Proof. Let $n$ be a natural number. If $n=1$ , then $n$ is the empty product of primes. If $n$ is prime, we are done. If $n$ is composite, then $n=ab$ with $a,b<n$ . By induction, $a$ and $b$ are products of primes, so $n$ is also a product of primes. $\qedsymbol$

Two questions immediately arise: (1) is this factorization unique, and (2) how quickly can we find such a factorization? Addressing (1), what if we had done something differently when breaking apart $1275$ as a product of primes? Could the primes that show up be different? Let's try: we have $1275 = 5\cdot 255$ . Now $255=5\cdot 51$ and $51=17\cdot 3$ , and again the factorization is the same, as asserted by Theorem 1.1.6 above. We will prove uniqueness of the prime factorization of any integer in Section 1.1.4.

SAGE Example 1.1   The command factor in SAGE factors an integer as a product of primes with multiplicities. For example,

sage: factor(1275)
3 * 5^2 * 17
sage: factor(2007)
3^2 * 223
sage: factor(31415926535898)
2 * 3 * 53 * 73 * 2531 * 534697

Regarding (2), there are algorithms for integer factorization. It is a major open problem to decide how fast integer factorization algorithms can be. We say that an algorithm to factor $n$ is polynomial time if there is a polynomial $f(x)$ such that for any $n$ the number of steps needed by the algorithm to factor $n$ is less than $f(\log_{10}(n))$ . Note that $\log_{10}(n)$ is an approximation for the number of digits of the input $n$ to the algorithm.

Open Problem 1.1   Is there an algorithm which can factor any integer $n$ in polynomial time?

Peter Shor [#!shor!#] devised a polynomial time algorithm for factoring integers on quantum computers. We will not discuss his algorithm further, except to note that in 2001 IBM researchers built a quantum computer that used Shor's algorithm to factor $15$ (see [#!quantum15!#,#!ibm:shor15!#]). Building much larger quantum computers appears to be extremely difficult.

You can earn money by factoring certain large integers. Many cryptosystems would be easily broken if factoring certain large integers were easy. Since nobody has proven that factoring integers is difficult, one way to increase confidence that factoring is difficult is to offer cash prizes for factoring certain integers. For example, until recently there was a $10000 bounty on factoring the following $174$ -digit integer (see [#!rsa:challenge!#]):

$$\begin{array}{l} 1881988129206079638386972394616504398071635... ...692321205734031879550656996221305168759307650257059 \end{array}$$

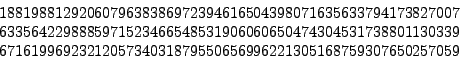
This number is known as RSA-576 since it has 576 digits when written in binary (see Section 2.3.2 for more on binary numbers). It was factored at the German Federal Agency for Information Technology Security in December 2003 (see [#!factor576!#]):

$$\begin{array}{l} 398075086424064937397125500550386491199064... ...459\\ \hspace{1ex}852171130520711256363590397527 \end{array}$$

The previous RSA challenge was the $155$ -digit number

$$\begin{array}{l} 1094173864157052742180970732204035761200373... ...2899781\\ 833797076537244027146743531593354333897. \end{array}$$

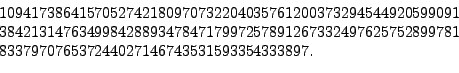
It was factored on 22 August 1999 by a group of sixteen researchers in four months on a cluster of 292 computers (see [#!rsa155!#]). They found that RSA-155 is the product of the following two $78$ -digit primes:

$$p = 10263959282974110577205419657399167590071656780803806$$

$$\hspace{4ex} 6803341933521790711307779$$

$$q = 10660348838016845482092722036001287867920795857598929$$

$$\hspace{4ex} 1522270608237193062808643.$$

The next RSA challenge is RSA-640:

$$\begin{array}{l} 3107418240490043721350750035888567930037346... ...772482278352574238645401469173660247765\\ 2346609, \end{array}$$

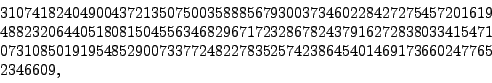
and its factorization was worth $20000 until November 2005 when it was factored by F. Bahr, M. Boehm, J. Franke, and T. Kleinjun. This factorization took 5 months. Here is one of the prime factors (you can find the other):

$$\begin{array}{l} 1634733645809253848443133883865090859841783... ...23121811108\\ 52389333100104508151212118167511579. \end{array}$$

(This team also factored a 663-bit RSA challenge integer.)

The smallest currently open challenge is RSA-704, worth $30000:

$$\begin{array}{l} 7403756347956171282804679609742957314259318... ...632990723963807867100\\ 86096962537934650563796359 \end{array}$$

SAGE Example 1.1   Using SAGE we see that the above number has 212 decimal digits and is definitely composite:

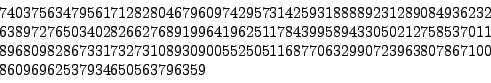
sage: n = 74037563479561712828046796097429573142593188889231289084936232638972765034028266276891996419625117843995894330502127585370118968098286733173273108930900552505116877063299072396380786710086096962537934650563796359
sage: len(n.str(2))
704
sage: len(n.str(10))
212
sage: n.is_prime()              # this is instant
False

These RSA numbers were factored using an algorithm called the number field sieve (see [#!lenstras:nfs!#]), which is the best-known general purpose factorization algorithm. A description of how the number field sieve works is beyond the scope of this book. However, the number field sieve makes extensive use of the elliptic curve factorization method, which we will describe in Section 6.3.