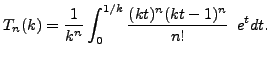5..
- If
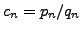 is the
is the  th convergent of
th convergent of
![$ [a_0,a_1,\ldots,a_n]$](img1561.png) and
and 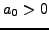 , show that
, show that
and
(Hint: In the first case, notice that
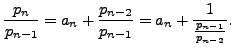 )
)
- Show that every nonzero rational number can be represented in
exactly two ways be a finite simple continued fraction. (For
example,
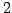 can be represented by
can be represented by ![$ [1,1]$](img2027.png) and
and ![$ [2]$](img2028.png) , and
, and 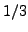 by
by ![$ [0,3]$](img2030.png) and
and ![$ [0,2,1]$](img2031.png) .)
.)
- Evaluate the infinite continued fraction
![$ [2,\overline{1,2,1}]$](img2032.png) .
.
- Determine the infinite continued fraction of
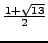 .
.
- Let
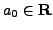 and
and
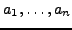 and
and 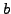 be positive
real numbers. Prove that
be positive
real numbers. Prove that
if and only if  is odd.
is odd.
- (*) Extend the method presented in the text
to show that the continued fraction expansion of
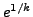 is
is
for all
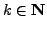 .
.
- Compute
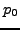 ,
, 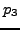 ,
, 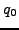 , and
, and 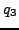 for the above continued fraction. Your answers should be in terms of
for the above continued fraction. Your answers should be in terms of 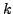 .
.
- Condense three steps of the recurrence for the numerators and denominators of the above continued fraction. That is, produce a simple recurrence for
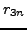 in terms of
in terms of 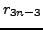 and
and 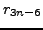 whose coefficients are polynomials in
whose coefficients are polynomials in  and
and 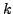 .
.
- Define a sequence of real numbers by
- Compute
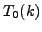 , and verify that it equals
, and verify that it equals
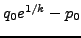 .
.
- Compute
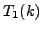 , and verify that it equals
, and verify that it equals
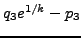 .
.
- Integrate
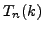 by parts twice in succession, as in
Section 5.3, and verify that
by parts twice in succession, as in
Section 5.3, and verify that 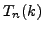 ,
,
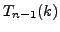 , and
, and
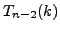 satisfy the recurrence produced in part 6b, for
satisfy the recurrence produced in part 6b, for 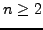 .
.
- Conclude that the continued fraction
represents 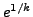 .
.
- Let
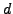 be an integer that is coprime to
be an integer that is coprime to 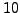 .
Prove that the decimal expansion of
.
Prove that the decimal expansion of
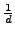 has period
equal to the order of
has period
equal to the order of 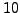 modulo
modulo 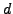 .
(Hint: For every positive integer
.
(Hint: For every positive integer 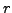 , we have
, we have
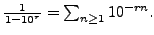 )
)
- Find a positive integer that has at least three
different representations as the sum of two squares, disregarding
signs and the order of the summands.
- Show that if a natural number
 is the sum of two
two rational squares it is also the sum of two integer squares.
is the sum of two
two rational squares it is also the sum of two integer squares.
- (*) Let
 be an odd prime. Show that
be an odd prime. Show that
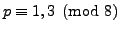 if and only if
if and only if  can be written as
can be written as
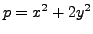 for
some choice of integers
for
some choice of integers 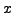 and
and 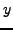 .
.
- Prove that of any four consecutive integers, at
least one is not representable as a sum of two squares.
William
2007-06-01
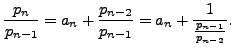 )
)