Next: Exercises Up: Elliptic Curves Over the Previous: The Torsion Subgroup of Contents Index
Every congruence class modulo ![]() except
except ![]() is represented in this
list, which incorrectly suggests that if
is represented in this
list, which incorrectly suggests that if
![]() then
then ![]() is
not a congruent number. Though no
is
not a congruent number. Though no ![]() with
with
![]() is a congruent number,
is a congruent number, ![]() is a congruent number congruent and
is a congruent number congruent and
![]() .
.
Deciding whether an integer ![]() is a congruent number can be subtle
since the simplest triangle with area
is a congruent number can be subtle
since the simplest triangle with area ![]() can be very complicated.
For example, as Zagier pointed out,
the number
can be very complicated.
For example, as Zagier pointed out,
the number ![]() is a congruent number, and
the ``simplest'' rational right triangle with area
is a congruent number, and
the ``simplest'' rational right triangle with area ![]() has side lengths
has side lengths
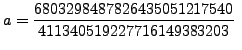 and
and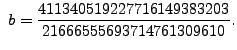
This solution would be difficult to find by a brute force search.
We call congruent numbers ``congruent'' because of the following proposition, which asserts that any congruent number is the common ``congruence'' between three perfect squares.
are all perfect squares of rational numbers.
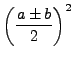 |
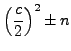 |
||
The main motivating open problem related to congruent numbers, is to give a systematic way to recognize them.
Fortunately, the vast theory developed about elliptic curves has something to say about the above problem. In order to understand this connection, we begin with an elementary algebraic proposition that establishes a link between elliptic curves and the congruent number problem.
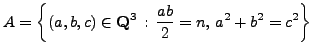
and
given explicitly by the maps
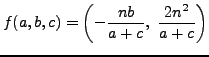
and
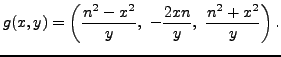
For ![]() , let
, let ![]() be the elliptic curve
be the elliptic curve
![]() .
.
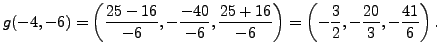
Multiplying through by
Observe that we can apply ![]() to any point in
to any point in
![]() with
with ![]() .
Using the group law we find that
.
Using the group law we find that
![]() ,
and
,
and
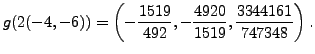
Example 6.5.9 foreshadows the following theorem.
Tunnell has proved that the Birch and Swinnerton-Dyer conjecture
(alluded to above), implies the existence of an elementary way to
decide whether or not an integer ![]() is a congruent number. We state
Tunnell's elementary way in the form of a conjecture.
is a congruent number. We state
Tunnell's elementary way in the form of a conjecture.
If
Enough of the Birch and Swinnerton-Dyer conjecture is known to prove
one direction of Conjecture 6.5.12. In particular, it is a
very deep theorem that if we do not have equality of the displayed
cardinalities, then ![]() is not a congruent
number. For example, when
is not a congruent
number. For example, when ![]() ,
,
The even more difficult (and still open!) part of
Conjecture 6.5.12 is the converse: If one has equality of the
displayed cardinalities, prove that ![]() is a congruent number. The
difficulty in this direction, which appears to be very deep, is that
we must somehow construct (or prove the existence of) elements of
is a congruent number. The
difficulty in this direction, which appears to be very deep, is that
we must somehow construct (or prove the existence of) elements of
![]() . This has been accomplished in some cases do to
groundbreaking work of Gross and Zagier ([#!gross-zagier!#]) but much
work remains to be done.
. This has been accomplished in some cases do to
groundbreaking work of Gross and Zagier ([#!gross-zagier!#]) but much
work remains to be done.
The excellent book [#!koblitz:cong!#] is about congruent numbers and Conjecture 6.5.12, and we encourage the reader to consult it. The Birch and Swinnerton-Dyer conjecture is a Clay Math Institute million dollar millennium prize problem (see [#!cmi!#,#!wiles:cmi!#]).
William 2007-06-01