


Next: The Main Results
Up: Component Groups of Purely
Previous: Component Groups of Purely
Let 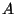 be an abelian variety over the rational numbers
be an abelian variety over the rational numbers
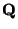 . Birch
and Swinnerton-Dyer found a conjectural formula for the order of the
Shafarevich-Tate group of
. Birch
and Swinnerton-Dyer found a conjectural formula for the order of the
Shafarevich-Tate group of 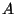 . The Tamagawa numbers
. The Tamagawa numbers 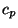 of
of 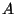 are
among the quantities that appear in this formula. We now recall the
definition of the Tamagawa numbers of an abelian variety
(the definition of Néron model and component groups
is given in Section 2).
are
among the quantities that appear in this formula. We now recall the
definition of the Tamagawa numbers of an abelian variety
(the definition of Néron model and component groups
is given in Section 2).
Definition 1.1 (Tamagawa number)
Let
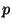
be a prime,
let
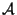
be the Néron model
of
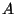
over the
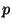
-adic integers
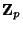
, and let
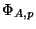
be the component group of
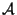
at
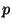
. Then the
Tamagawa number 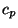
of
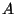
at
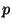
is the order of the subgroup
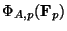
of
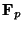
-rational points
in
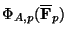
.
Remark 1.2
The Tamagawa number is defined in a different way in some other
papers, but the definitions are equivalent.
When 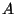 has dimension one,
has dimension one, 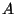 is called an elliptic curve, and
is called an elliptic curve, and 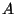 can be defined by a Weierstrass equation
can be defined by a Weierstrass equation
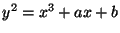 . Using that
elliptic curves (and their related integral models) can be described by simple
equations, Tate found an efficient algorithm to compute all of the
Tamagawa numbers of
. Using that
elliptic curves (and their related integral models) can be described by simple
equations, Tate found an efficient algorithm to compute all of the
Tamagawa numbers of 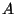 (see [18]).
In the case when
(see [18]).
In the case when
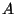 is the Jacobian of a genus
is the Jacobian of a genus 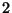 curve, [7] discusses a
method for computing the Tamagawa numbers of
curve, [7] discusses a
method for computing the Tamagawa numbers of 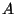 . In this paper, we
consider the situation in which
. In this paper, we
consider the situation in which 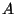 has purely toric reduction at
has purely toric reduction at 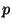 ,
with no constraint on the dimension of
,
with no constraint on the dimension of 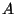 . For such
. For such 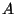 we give an
explicit description of the order of the group of connected
components of the closed fiber of the Néron model of
we give an
explicit description of the order of the group of connected
components of the closed fiber of the Néron model of 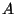 .
In the case when
.
In the case when 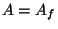 is a quotient of
is a quotient of  attached to a newform
attached to a newform
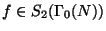 and
and
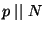 , our method is
completely explicit, and yields an algorithm to compute the Tamagawa
number
, our method is
completely explicit, and yields an algorithm to compute the Tamagawa
number 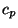 of
of 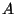 (up to a bounded power of
(up to a bounded power of 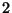 ).
).
This paper is structured as follows. In
Sections 2-6 we state
and prove an explicit formula involving component groups of fairly
general abelian varieties. Then in Section 7 we turn
to quotients of modular Jacobians  . We give some tables and
discussed the arithmetic of quotients of
. We give some tables and
discussed the arithmetic of quotients of  when
when  is
prime. In Section 8 we prove a couple of facts about
toric reduction that are used in the proof of Theorem 6.1.
is
prime. In Section 8 we prove a couple of facts about
toric reduction that are used in the proof of Theorem 6.1.
Acknowledgement: This paper was inspired by lectures of
R. Coleman and K. Ribet, and a letter from Ribet to Mestre (see
[17]), which contains some of the results of
the present paper in the case when 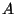 has dimension
has dimension 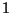 .
The second author would like to thank A. Abbes, A. Agashe, D. Kohel, and
D. Lorenzini, for helpful conversations. Both authors were partially
supported by the NSF and the Clay Mathematics Institute during
work on this paper.
.
The second author would like to thank A. Abbes, A. Agashe, D. Kohel, and
D. Lorenzini, for helpful conversations. Both authors were partially
supported by the NSF and the Clay Mathematics Institute during
work on this paper.



Next: The Main Results
Up: Component Groups of Purely
Previous: Component Groups of Purely
William A Stein
2001-12-09
![]() . We give some tables and
discussed the arithmetic of quotients of
. We give some tables and
discussed the arithmetic of quotients of ![]() when
when ![]() is
prime. In Section 8 we prove a couple of facts about
toric reduction that are used in the proof of Theorem 6.1.
is
prime. In Section 8 we prove a couple of facts about
toric reduction that are used in the proof of Theorem 6.1.
![]() has dimension
has dimension ![]() .
The second author would like to thank A. Abbes, A. Agashe, D. Kohel, and
D. Lorenzini, for helpful conversations. Both authors were partially
supported by the NSF and the Clay Mathematics Institute during
work on this paper.
.
The second author would like to thank A. Abbes, A. Agashe, D. Kohel, and
D. Lorenzini, for helpful conversations. Both authors were partially
supported by the NSF and the Clay Mathematics Institute during
work on this paper.