


Next: The Quadratic Reciprocity Law
Up: Lecture 12: Quadratic Reciprocity
Previous: Lecture 12: Quadratic Reciprocity
Proposition 1.1 (Euler's Criterion)
Let
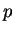
be an odd prime and
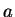
an integer not divisible by
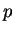
.
Then
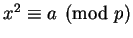
has a solution if and only if
Proof.
By the theorem from Lecture 11, there is an integer
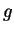
that
has order
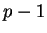
modulo
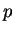
. Every integer coprime to
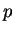
is
congruent to a power of
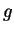
.
First suppose that
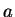
is congruent to a perfect square modulo
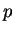
,
so
for some
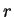
. Then
Conversely, suppose that
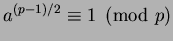
. We have
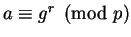
for some integer
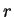
.
Thus
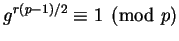
, so
which implies that
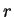
is even.
Thus
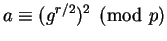
, so
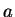
is congruent to a square modulo
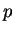
.

Corollary 1.2
If
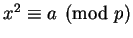
has no solutions if and only if
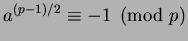
.
Proof.
This follows from Proposition
1.1 and that
the polynomial
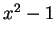
has no roots besides
and
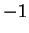
.

Example 1.3
Suppose
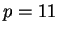
.
By squaring each element of
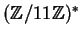
, we see
exactly which numbers are squares modulo
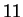
:
Thus the squares are
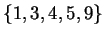
.
Next, we compute

for each
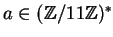
.
The
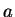
with
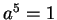
are
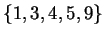
, which is exactly the
same as the set of squares, just as Proposition
1.1
predicts.
Example 1.4
Determine whether or not
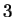
is a square
modulo
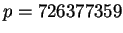
.
Answer:
We compute
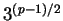
modulo
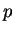
using PARI:
? Mod(3,p)^((p-1)/2)
%5 = Mod(726377358, 726377359) \\ class of -1 modulo 726377359.
Thus
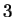
is not a square modulo
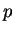
. This computation wasn't too
difficult, but it would have been very tedious to carry about by hand.
The law of quadratic reciprocity, which we will state in the next section,
is a vastly more powerful way to answer such questions.
For example, you could easily answer the above question
by hand using quadratic reciprocity.
Remark 1.5
Proposition
1.1 can be reformulated in more group-theoretic
language as follows. The map
that sends
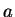
to
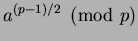
is a homomorphism of groups, whose kernel is
the subgroup of squares of elements of
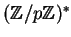
.
Definition 1.6
An element
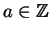
with
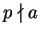
is called a
quadratic
residue modulo
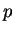
if
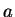
is a square modulo
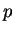
.



Next: The Quadratic Reciprocity Law
Up: Lecture 12: Quadratic Reciprocity
Previous: Lecture 12: Quadratic Reciprocity
William A Stein
2001-10-06