

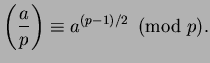
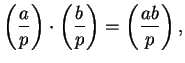
The symbol
![]() only depends on the residue class
of
only depends on the residue class
of ![]() modulo
modulo ![]() . Thus tabulating the value of
. Thus tabulating the value of
![]() for hundreds of
for hundreds of ![]() would be silly.
Would it be equally silly to make a table of
would be silly.
Would it be equally silly to make a table of
![]() for hundreds of primes
for hundreds of primes ![]() ? Let's begin making such a table
and see whether or not there is an obvious pattern.
(To compute
? Let's begin making such a table
and see whether or not there is an obvious pattern.
(To compute
![]() in PARI, use the command kronecker(a,b).)
in PARI, use the command kronecker(a,b).)
|
|
||
| 7 | 2 | |
| 11 | 1 | |
| 13 | 3 | |
| 17 | 2 | |
| 19 | 4 | |
| 23 | 3 | |
| 29 | 4 | |
| 31 | 1 | |
| 37 | 2 | |
| 41 | 1 | |
| 43 | 3 | |
| 47 | 2 |
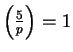 if and only
if
if and only
if
Based on such computations, various mathematicians found a conjectural explanation for this mystery in the 18th century. Finally, on April 8, 1796, at your age (age 19), Gauss proved their conjecture.
We will prove this theorem in the next lecture.
In the case considered above, this theorem implies that
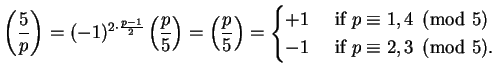
Here is a list of almost 200 proofs of Theorem 2.1:
http://www.rzuser.uni-heidelberg.de/~hb3/rchrono.html