How Many Primes are There?

We saw in Section 1.2.1 that there are infinitely many primes. In order to get a sense for just how many primes there are, we consider a few warm-up questions. Then we consider some numerical evidence and state the prime number theorem, which gives an asymptotic answer to our question, and connect this theorem with a form of the famous Riemann Hypothesis. Our discussion of counting primes in this section is very cursory; for more details, read Crandall and Pomerance's excellent book [#!primenumbers!#, §1.1.5].

The following vague discussion is meant to motivate a precise way to measure the number (or percentage) of primes. What percentage of natural numbers are even? Answer: Half of them. What percentage of natural numbers are of the form $4x-1$ ? Answer: One fourth of them. What percentage of natural numbers are perfect squares? Answer: Zero percent of all natural numbers, in the sense that the limit of the proportion of perfect squares to all natural numbers converges to 0 . More precisely,

$$\lim_{x\rightarrow \infty} \frac{\char93 \{n\in\mathbb {N}: n \leq x \text{ and $n$ is a perfect square}\}}{x} = 0,$$

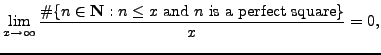
since the numerator is roughly $\sqrt{x}$ and $\lim_{x\rightarrow \infty}\frac{\sqrt{x}}{x} = 0$ . Likewise, it is an easy consequence of Theorem 1.2.11 below that zero percent of all natural numbers are prime (see Exercise 1.4).

We are thus led to ask another question: How many positive integers $\leq x$ are perfect squares? Answer: roughly $\sqrt{x}$ . In the context of primes, we ask,

Question 1.2   How many natural numbers $\leq x$ are prime?

Let

$$\pi(x) = \char93 \{p\in \mathbb {N}: p \leq x$$    is a prime$$\}.$$

For example,

$$\pi(6) =\char93 \{2,3,5\} = 3.$$

Some values of $\pi(x)$ are given in Table 1.1, and Figures 1.1 and 1.2 contain graphs of $\pi(x)$ . These graphs look like straight lines, which maybe bend down slightly.

SAGE Example 1.2   To compute $\pi(x)$ in SAGE use the command prime_pi(x):

sage: prime_pi(6)
3
sage: prime_pi(100)
25
sage: prime_pi(3000000)
216816

We can also draw a plot of $\pi(x)$ using the plot command:

sage.: show(plot(prime_pi, 1,1000, rgbcolor=(0,0,1)))

Table 1.1: Values of $\pi(x)$

$x$	100	200	300	400	500	600	700	800	900	1000
$\pi(x)$	25	46	62	78	95	109	125	139	154	168

Figure 1.1: Graph of $\pi(x)$ for $x<1000$

Gauss was an inveterate computer: he wrote in an 1849 letter that there are $216,745$ primes less than $3,000,000$ (this is wrong but close; the correct count is $216,816$ ).

Gauss conjectured the following asymptotic formula for $\pi(x)$ , which was later proved independently by Hadamard and Vallée Poussin in 1896 (but will not be proved in this book):

Theorem 1.2 (Prime Number Theorem)   The function $\pi(x)$ is asymptotic to $x/\log(x)$ , in the sense that

$$\lim_{x\rightarrow \infty} \frac{\pi(x)}{ x/\log(x)} = 1.$$

We do nothing more here than motivate this deep theorem with a few further observations. The theorem implies that

$$\lim_{x\rightarrow \infty} \frac{\pi(x)}{x} = \lim_{x\rightarrow \infty} \frac{1}{\log(x)} =0,$$

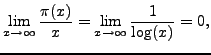
so for any $a$ ,

$$\lim_{x\rightarrow \infty} \frac{\pi(x)}{x/(\log(x)-a)} = \lim_{x\rightarrow \infty} \frac{\pi(x)}{x/\log(x)} - \frac{a\pi(x)}{x} = 1.$$

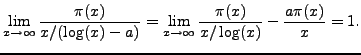
Thus $x/(\log(x)-a)$ is also asymptotic to $\pi(x)$ for any $a$ . See [#!primenumbers!#, §1.1.5] for a discussion of why $a=1$ is the best choice. Table 1.2 compares $\pi(x)$ and $x/(\log(x)-1)$ for several $x<10000$ .

Table 1.2: Comparison of $\pi(x)$ and $x/(\log(x)-1)$

$\quad{}\!x$	$\pi(x)$	$x/(\log(x)-1)$ (approx)
1000	168	169.2690290604408165186256278
2000	303	302.9888734545463878029800994
3000	430	428.1819317975237043747385740
4000	550	548.3922097278253264133400985
5000	669	665.1418784486502172369455815
6000	783	779.2698885854778626863677374
7000	900	891.3035657223339974352567759
8000	1007	1001.602962794770080754784281
9000	1117	1110.428422963188172310675011
10000	1229	1217.976301461550279200775705

Figure 1.2: Graphs of $\pi(x)$ for $x<10000$ and $x<100000$

As of 2004, the record for counting primes appears to be

$$\pi(4\cdot 10^{22}) = 783964159847056303858.$$

The computation of $\pi(4\cdot 10^{22})$ reportedly took ten months on a 350 Mhz Pentium II (see [#!pixproject!#] for more details).

For the reader familiar with complex analysis, we mention a connection between $\pi(x)$ and the Riemann Hypothesis. The Riemann zeta function $\zeta(s)$ is a complex analytic function on $\mathbb{C}\setminus \{1\}$ that extends the function defined on a right half plane by $\sum_{n=1}^{\infty} n^{-s}$ . The Riemann Hypothesis is the conjecture that the zeros in $\mathbb {C}$ of $\zeta(s)$ with positive real part lie on the line ${\rm Re}(s)=1/2$ . This conjecture is one of the Clay Math Institute million dollar millennium prize problems [#!cmi!#].

According to [#!primenumbers!#, §1.4.1], the Riemann Hypothesis is equivalent to the conjecture that

$$\Li (x) = \int_{2}^{x} \frac{1}{\log(t)} dt$$

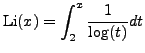
is a ``good'' approximation to $\pi(x)$ , in the following precise sense:

Conjecture 1.2 (Equivalent to the Riemann Hypothesis)  
For all $x\geq 2.01$ ,

$$\vert\pi(x)-\Li (x)\vert \leq \sqrt{x}\log(x).$$

If $x=2$ , then $\pi(2)=1$ and $\Li (2)=0$ , but $\sqrt{2}\log(2) = 0.9802\ldots$ , so the inequality is not true for $x\geq 2$ , but $2.01$ is big enough. We will do nothing more to explain this conjecture, and settle for one numerical example.

Example 1.2   Let $x=4\cdot 10^{22}$ . Then

$$\pi(x) = 783964159847056303858,$$

$$\Li (x) = 783964159852157952242.7155276025801473\ldots,$$

$$\vert\pi(x) - \Li (x)\vert = 5101648384.71552760258014\ldots,$$

$$\sqrt{x}\log(x) = 10408633281397.77913344605\ldots,$$

$$x/(\log(x)-1) = 783650443647303761503.5237113087392967\ldots.$$

SAGE Example 1.2   We use SAGE to graph $\pi(x)$ , $\Li (x)$ , and $\sqrt{x}\log(x)$ .

sage: def Li(x):
...   return integral_numerical(lambda t: 1/log(t), 2, x)[0]
sage: P = plot(prime_pi, 2,10000, rgbcolor=(1,0,0),plot_points=30)
sage: Q = plot(Li, 2,10000, rgbcolor=(0,0,1), plot_points=30)
sage: R = plot(lambda x: sqrt(x)*log(x), 2, 10000)
sage.: show(P+Q+R,xmin=0)

For more on the prime number theorem and the Riemann hypothesis see [#!zagier:primes50!#] and [#!mazur-stein:rh!#].