1..
- Compute the greatest common divisor
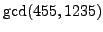 by hand.
by hand.
- Use the Sieve of Eratosthenes
to make a list of all primes up to
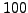 .
.
- Prove that there are infinitely
many primes of the form
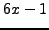 .
.
- Use Theorem 1.2.11 to deduce that
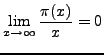 .
.
- Let
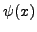 be the number of primes of the form
be the number of primes of the form
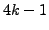 that are
that are 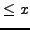 . Use a computer to make a conjectural
guess about
. Use a computer to make a conjectural
guess about
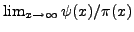 .
.
- So far
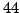 Mersenne primes
Mersenne primes 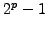 have been discovered.
Give a guess, backed up by an argument, about
when the next Mersenne prime might be discovered (you will have
to do some online research).
have been discovered.
Give a guess, backed up by an argument, about
when the next Mersenne prime might be discovered (you will have
to do some online research).
- Let
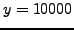 . Compute
. Compute
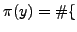 primes
primes 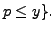
- The prime number theorem implies
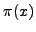 is
asymptotic to
is
asymptotic to
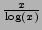 . How close is
. How close is 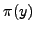 to
to
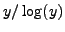 , where
, where 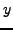 is as in (a)?
is as in (a)?
- Let
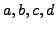 , and
, and 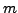 be integers. Prove that
be integers. Prove that
- if
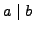 and
and 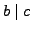 then
then 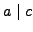 ,
,
- if
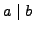 and
and 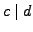 then
then 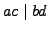 ,
,
- if
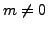 , then
, then 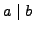 if and only if
if and only if 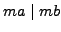 , and
, and
- if
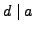 and
and 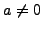 , then
, then
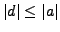 .
.
- In each of the following, apply the division algorithm
to find
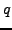 and
and 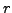 such that
such that
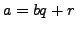 and
and
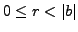 :
:
- (Do this part by hand.) Compute the greatest common
divisor of
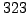 and
and 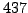 using the algorithm described in class
that involves quotients and remainders (i.e., do not just factor
using the algorithm described in class
that involves quotients and remainders (i.e., do not just factor  and
and 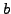 ).
).
- Compute by any means the greatest common divisor
- Suppose
 ,
, 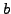 and
and  are positive integers. Prove
that if
are positive integers. Prove
that if
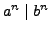 , then
, then 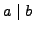 .
.
- Suppose
 is a prime and
is a prime and  and
and 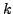 are positive
integers. Prove that if
are positive
integers. Prove that if
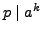 , then
, then
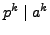 .
.
- Prove that if a positive integer
 is a perfect
square, then
is a perfect
square, then  cannot be written in the form
cannot be written in the form 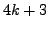 for
for 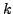 an integer.
(Hint: Compute the remainder upon division
by
an integer.
(Hint: Compute the remainder upon division
by 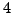 of each of
of each of 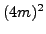 ,
, 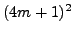 ,
, 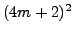 ,
and
,
and 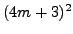 .)
.)
- Prove that no integer in the sequence
is a perfect square. (Hint:
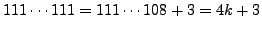 .)
.)
- Prove that a positive integer
 is prime if
and only if
is prime if
and only if  is not divisible by any prime
is not divisible by any prime  with
with
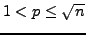 .
.
William
2007-06-01
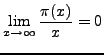 .
.