Next: Factoring Given Up: Attacking RSA Previous: Factoring Given Contents Index
Suppose ![]() with
with ![]() , say. Then
, say. Then
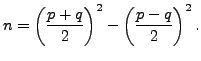
Since
is small,
is only slightly larger than
until
If ![]() , then
, then
![]() .
.
If ![]() , then
, then
![]() .
.
If ![]() , then
, then
![]() .
.
Thus ![]() . We find that
. We find that
![]() and
and
![]() .
.
sage: def crack_when_pq_close(n): ... t = Integer(ceil(sqrt(n))) ... while True: ... k = t^2 - n ... if k > 0: ... s = Integer(int(round(sqrt(t^2 - n)))) ... if s^2 + n == t^2: ... return t+s, t-s ... ... t += 1 ... sage: crack_when_pq_close(23360947609) (153649, 152041)
For example, you might think that choosing a random prime, and the next prime after would be a good idea, but instead it creates an easy-to-crack crpytosystem.
sage: p = next_prime(2^128); p
340282366920938463463374607431768211507
sage: q = next_prime(p)
sage: crack_when_pq_close(p*q)
(340282366920938463463374607431768211537,
340282366920938463463374607431768211507)
William 2007-06-01