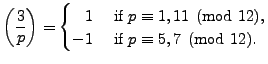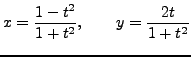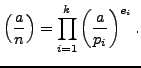4..
- Calculate the following by hand:
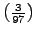 ,
,
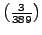 ,
,
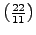 , and
, and
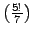 .
.
- Let
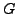 be an abelian group
and let
be an abelian group
and let  be a positive integer.
be a positive integer.
- Prove that the
map
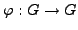 given by
given by
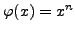 is a group
homomorphism.
is a group
homomorphism.
- Prove that the subset
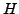 of
of 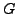 of squares
of elements of
of squares
of elements of 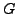 is a subgroup.
is a subgroup.
- Use Theorem 4.1.7
to show that for
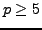 prime,
prime,
- (*) Use that
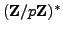 is cyclic to give a
direct proof that
is cyclic to give a
direct proof that
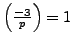 when
when
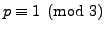 . (Hint:
There is an
. (Hint:
There is an
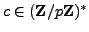 of order
of order 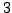 . Show that
. Show that
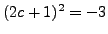 .)
.)
- (*) If
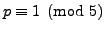 , show directly that
, show directly that
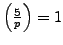 by the method of Exercise 4.4.
(Hint: Let
by the method of Exercise 4.4.
(Hint: Let
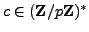 be an element of order
be an element of order 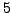 . Show that
. Show that
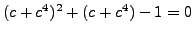 , etc.)
, etc.)
- (*) Let
 be an odd prime. In this exercise you
will prove that
be an odd prime. In this exercise you
will prove that
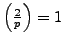 if and only if
if and only if
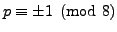 .
.
- Prove that
is a parameterization of the set of solutions to
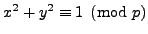 ,
in the sense that the solutions
,
in the sense that the solutions
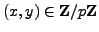 are in
bijection with the
are in
bijection with the
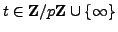 such that
such that
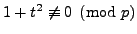 .
Here
.
Here 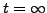 corresponds to the point
corresponds to the point 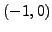 .
(Hint: if
.
(Hint: if 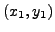 is a solution, consider the line
is a solution, consider the line 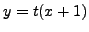 through
through 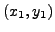 and
and 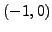 , and solve for
, and solve for 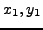 in terms
of
in terms
of 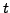 .)
.)
- Prove that the number of solutions to
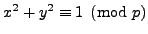 is
is 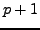 if
if
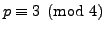 and
and 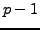 if
if
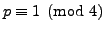 .
.
- Consider the set
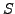 of pairs
of pairs
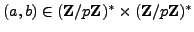 such
that
such
that 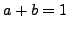 and
and
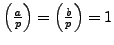 . Prove that
. Prove that
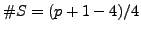 if
if
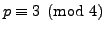 and
and
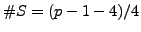 if
if
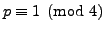 . Conclude that
. Conclude that 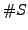 is odd if and only if
is odd if and only if
- The map
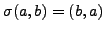 that swaps coordinates is a
bijection of the set
that swaps coordinates is a
bijection of the set 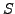 . It has exactly one fixed point if and
only if there is an
. It has exactly one fixed point if and
only if there is an
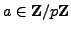 such that
such that 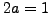 and
and
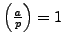 .
Also, prove that
.
Also, prove that 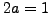 has a solution
has a solution
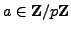 with
with
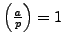 if and only if
if and only if
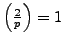 .
.
- Finish by showing that
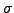 has exactly one fixed point
if and only if
has exactly one fixed point
if and only if 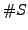 is odd, i.e., if and only if
is odd, i.e., if and only if
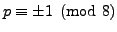 .
.
Remark: The method of proof of this exercise can be generalized to give a
proof of the full quadratic reciprocity law.
- How many natural numbers
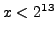 satisfy the
equation
satisfy the
equation
You may assume that 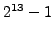 is prime.
is prime.
- Find the natural number
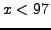 such that
such that
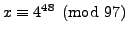 . Note that
. Note that 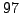 is prime.
is prime.
- In this problem we will formulate an analogue of
quadratic reciprocity for a symbol like
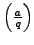 , but without the
restriction that
, but without the
restriction that 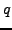 be a prime. Suppose
be a prime. Suppose  is a positive integer,
which we factor as
is a positive integer,
which we factor as
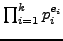 . We
define the Jacobi symbol
. We
define the Jacobi symbol
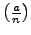 as follows:
as follows:
- Give an example to show that
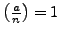 need not imply that
need not imply that
 is a perfect square modulo
is a perfect square modulo  .
.
- (*) Let
 be odd and
be odd and  and
and 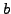 be integers. Prove that the
following holds:
be integers. Prove that the
following holds:
-
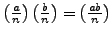 . (Thus
. (Thus
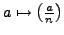 induces a homomorphism from
induces a homomorphism from
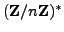 to
to 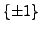 .)
.)
-
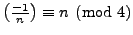 .
.
-
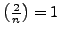 if
if
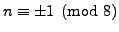 and
and 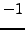 otherwise.
otherwise.
-
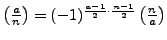
- (*) Prove that for any
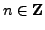 the integer
the integer
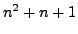 does not have any divisors of the form
does not have any divisors of the form 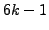 .
.
William
2007-06-01