Examples
For simplicity, we use an elliptic curve of the form
which has the point 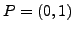 already on it.
already on it.
We factor 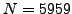 using the elliptic curve method.
Let
using the elliptic curve method.
Let
where 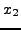 means
means 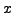 is written in binary.
First we choose
is written in binary.
First we choose 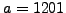 at random and consider
at random and consider
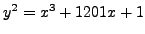 over
over
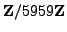 .
Using the formula for
.
Using the formula for 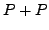 from
Algorithm 6.2.1
we compute
from
Algorithm 6.2.1
we compute
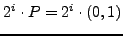 for
for
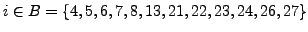 .
Then
.
Then
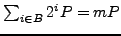 . It turns out that during no
step of this computation does a number not coprime to
. It turns out that during no
step of this computation does a number not coprime to
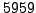 appear in any denominator, so we do not split
appear in any denominator, so we do not split 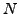 using
using 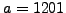 . Next we try
. Next we try 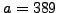 and at some stage
in the computation we add
and at some stage
in the computation we add
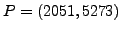 and
and
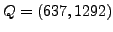 .
When computing the group law explicitly we try
to compute
.
When computing the group law explicitly we try
to compute
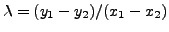 in
in
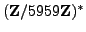 ,
but fail since
,
but fail since
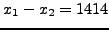 and
and
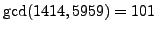 .
We thus find a nontrivial factor
.
We thus find a nontrivial factor 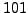 of
of 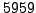 .
.
William
2007-06-01
![]() using the elliptic curve method.
Let
using the elliptic curve method.
Let