A Heuristic Explanation
Let 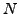 be a positive integer and for simplicity of exposition
assume that
be a positive integer and for simplicity of exposition
assume that
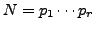 with the
with the 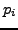 distinct primes.
It follows from Lemma 2.2.6 that there is a
natural isomorphism
distinct primes.
It follows from Lemma 2.2.6 that there is a
natural isomorphism
When using Pollard's method, we choose an
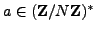 ,
compute
,
compute 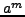 , then compute
, then compute
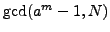 . This
. This 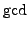 is divisible
exactly by the primes
is divisible
exactly by the primes 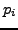 such that
such that
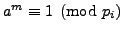 . To
reinterpret Pollard's method using the above isomorphism, let
. To
reinterpret Pollard's method using the above isomorphism, let
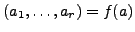 . Then
. Then
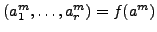 , and
the
, and
the 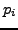 that divide
that divide
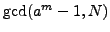 are exactly the
are exactly the 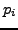 such that
such that
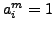 . By Theorem 2.1.19, these
. By Theorem 2.1.19, these 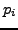 include the
primes
include the
primes 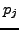 such that
such that 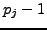 is
is 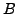 -power smooth, where
-power smooth, where
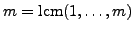 .
.
We will not define
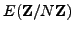 when
when 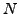 is composite, since this is
not needed for the algorithm (where we assume that
is composite, since this is
not needed for the algorithm (where we assume that 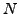 is prime and
hope for a contradiction). However, for the remainder of this
paragraph, we pretend that
is prime and
hope for a contradiction). However, for the remainder of this
paragraph, we pretend that
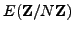 is meaningful and describe a
heuristic connection between Lenstra and Pollard's methods. The
significant difference between Pollard's method and the elliptic curve
method is that the isomorphism
is meaningful and describe a
heuristic connection between Lenstra and Pollard's methods. The
significant difference between Pollard's method and the elliptic curve
method is that the isomorphism 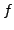 is replaced by an isomorphism (in quotes)
is replaced by an isomorphism (in quotes)
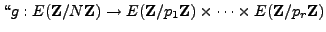
''
where 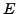 is
is
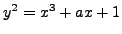 , and the
, and the  of Pollard's method is
replaced by
of Pollard's method is
replaced by 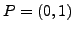 . We put the isomorphism in quotes to emphasize
that we have not defined
. We put the isomorphism in quotes to emphasize
that we have not defined
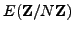 . When carrying out the
elliptic curve factorization algorithm, we attempt to compute
. When carrying out the
elliptic curve factorization algorithm, we attempt to compute 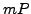 and
if some components of
and
if some components of 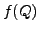 are
are 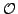 , for some point
, for some point 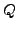 that appears
during the computation, but others are nonzero, we find a nontrivial
factor of
that appears
during the computation, but others are nonzero, we find a nontrivial
factor of 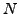 .
.
William
2007-06-01
![]() when
when ![]() is composite, since this is
not needed for the algorithm (where we assume that
is composite, since this is
not needed for the algorithm (where we assume that ![]() is prime and
hope for a contradiction). However, for the remainder of this
paragraph, we pretend that
is prime and
hope for a contradiction). However, for the remainder of this
paragraph, we pretend that
![]() is meaningful and describe a
heuristic connection between Lenstra and Pollard's methods. The
significant difference between Pollard's method and the elliptic curve
method is that the isomorphism
is meaningful and describe a
heuristic connection between Lenstra and Pollard's methods. The
significant difference between Pollard's method and the elliptic curve
method is that the isomorphism ![]() is replaced by an isomorphism (in quotes)
is replaced by an isomorphism (in quotes)