Recognizing Rational Numbers From Their Decimal Expansion

Suppose that somehow you can compute approximations to some rational number, and want to figure what the rational number probably is. Computing the approximation to high enough precision to find a period in the decimal expansion is not a good approach, because the period can be huge (see below). A much better approach is to compute the simple continued fraction of the approximation, and truncate it before a large partial quotient $a_n$ , then compute the value of the truncated continued fraction. This results in a rational number that has relatively small numerator and denominator, and is close to the approximation of the rational number, since the tail end of the continued fraction is at most $1/a_n$ .

We begin with a contrived example, which illustrates how to recognize a rational number. Let

$$x=9495/3847 = 2.46815700545879906420587470756433584611385\ldots.$$

The continued fraction of the truncation $2.468157005458799064$ is

$$[2, 2, 7, 2, 1, 5, 1, 1, 1, 1, 1, 1, 328210621945, 2, 1, 1, 1, \ldots ]$$

We have

$$[2, 2, 7, 2, 1, 5, 1, 1, 1, 1, 1, 1] = \frac{9495}{3847}.$$

Notice that no repetition is evident in the digits of $x$ given above, though we know that the decimal expansion of $x$ must be eventually periodic, since all decimal expansions of rational numbers are eventually periodic. In fact, the length of the period of the decimal expansion of $1/3847$ is $3846$ , which is the order of $10$ modulo $3847$ (see Exercise 5.7).

For a slightly less contrived application of this idea, suppose $f(x)\in\mathbb{Z}[x]$ is a polynomial with integer coefficients, and we know for some reason that one root of $f$ is a rational number. Then we can find that rational number by using Newton's method to approximate each root, and continued fractions to decide whether each root is a rational number (we can substitute the value of the continued fraction approximation into $f$ to see if it is actually a root). One could also use the well-known rational root theorem, which asserts that any rational root $n/d$ of $f$ , with $n,d\in\mathbb{Z}$ coprime, has the property that $n$ divides the constant term of $f$ and $d$ the leading coefficient of $f$ . However, using that theorem to find $n/d$ would require factoring the constant and leading terms of $f$ , which could be completely impractical if they have a few hundred digits (see Section 1.1.3). In contrast, Newton's method and continued fractions should quickly find $n/d$ , assuming the degree of $f$ isn't too large.

For example, suppose $f=3847x^2 - 14808904x + 36527265$ . To apply Newton's method, let $x_0$ be a guess for a root of $f$ . Then iterate using the recurrence

$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}.$$

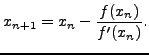
Choosing $x_0 = 0$ , approximations of the first two iterates are

$$x_1 = 2.466574501394566404103909378,$$

and

$$x_2 = 2.468157004807401923043166846.$$

The continued fraction of the approximations $x_1$ and $x_2$ are

$$[2, 2, 6, 1, 47, 2, 1, 4, 3, 1, 5, 8, 2, 3]$$

and

$$[2, 2, 7, 2, 1, 5, 1, 1, 1, 1, 1, 1, 103, 8, 1, 2, 3, \ldots].$$

Truncating the continued fraction of $x_2$ before $103$ gives

$$[2, 2, 7, 2, 1, 5, 1, 1, 1, 1, 1, 1],$$

which evaluates to $9495/3847$ , which is a rational root of $f$ .

SAGE Example 5.5   We do the above calculation using SAGE. First we implement Newton iteration:

sage: def newton_root(f, iterates=2, x0=0, prec=53):
...    x = RealField(prec)(x0)
...    R = PolynomialRing(ZZ,'x')
...    f = R(f)
...    g = f.derivative()
...    for i in range(iterates):
...        x = x - f(x)/g(x)
...    return x

Next we run the Newton iteration, and compute the continued fraction of the result:

sage: a = newton_root(3847*x^2 - 14808904*x + 36527265); a
2.46815700480740
sage: cf = continued_fraction(a); cf
[2, 2, 7, 2, 1, 5, 1, 1, 1, 1, 1, 1, 103, 8, 1, 2, 3, 1, 1]

We truncate the continued fraction and compute its value.

sage: c = cf[:12]; c
[2, 2, 7, 2, 1, 5, 1, 1, 1, 1, 1, 1]
sage: c.value()
9495/3847

Another computational application of continued fractions, which we can only hint at, is that there are functions in certain parts of advanced number theory (that are beyond the scope of this book) that take rational values at certain points, and which can only be computed efficiently via approximations; using continued fractions as illustrated above to evaluate such functions is crucial.